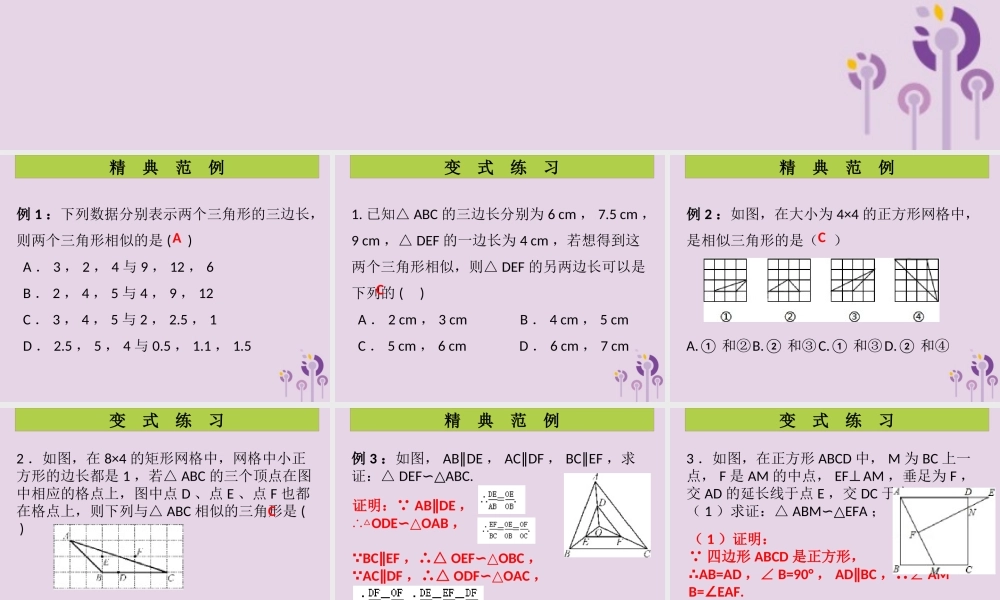
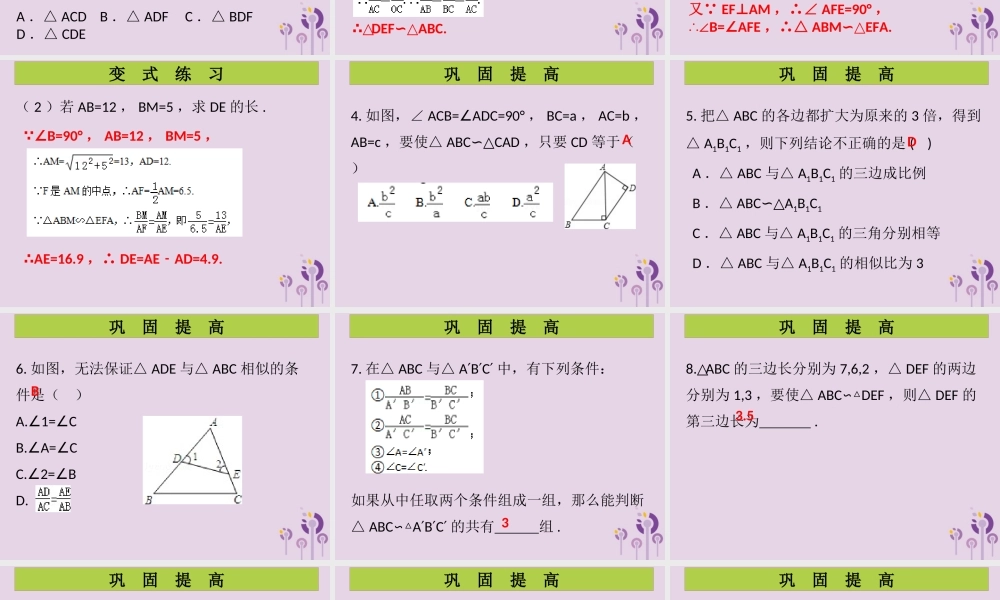
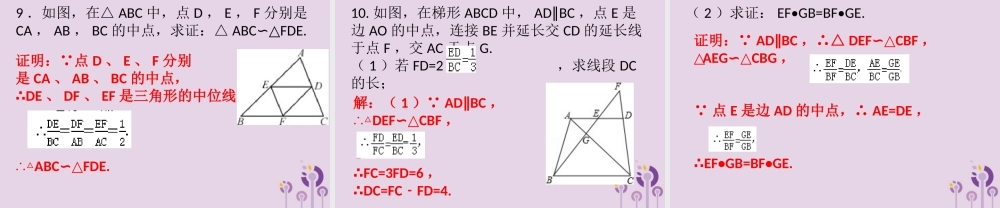
第 7 课时 探索相似三角形的条件( 3 )巩固提高精典范例(变式练习)第四章 图形的相似例 1 :下列数据分别表示两个三角形的三边长,则两个三角形相似的是 ( ) A . 3 , 2 , 4 与 9 , 12 , 6 B . 2 , 4 , 5 与 4 , 9 , 12 C . 3 , 4 , 5 与 2 , 2.5 , 1 D . 2.5 , 5 , 4 与 0.5 , 1.1 , 1.5精 典 范 例A1. 已知△ ABC 的三边长分别为 6 cm , 7.5 cm ,9 cm ,△ DEF 的一边长为 4 cm ,若想得到这两个三角形相似,则△ DEF 的另两边长可以是下列的 ( ) A . 2 cm , 3 cm B . 4 cm , 5 cm C . 5 cm , 6 cm D . 6 cm , 7 cm变 式 练 习C例 2 :如图,在大小为 4×4 的正方形网格中,是相似三角形的是( )A.① 和②B.② 和③C.① 和③D.② 和④精 典 范 例C2 .如图,在 8×4 的矩形网格中,网格中小正方形的边长都是 1 ,若△ ABC 的三个顶点在图中相应的格点上,图中点 D 、点 E 、点 F 也都在格点上,则下列与△ ABC 相似的三角形是 ( )A .△ ACD B .△ ADF C .△ BDF D .△ CDE变 式 练 习C例 3 :如图, AB DE∥, AC DF∥, BC EF∥,求证:△ DEFABC.∽△精 典 范 例证明: AB DE∥,∴△ODEOAB∽△, BC EF∥,∴△ OEFOBC∽△, AC DF∥,∴△ ODFOAC∽△,∴△DEFABC.∽△3 .如图,在正方形 ABCD 中, M 为 BC 上一点, F 是 AM 的中点, EF⊥AM ,垂足为 F ,交 AD 的延长线于点 E ,交 DC 于点 N.( 1 )求证:△ ABMEFA∽△;变 式 练 习( 1 )证明: 四边形 ABCD 是正方形,∴AB=AD ,∠ B=90° , AD BC∥,∴∠ AMB=EAF.∠又 EFAM⊥,∴∠ AFE=90° ,∴∠B=AFE∠,∴△ ABMEFA.∽△变 式 练 习( 2 )若 AB=12 , BM=5 ,求 DE 的长 . ∠B=90° , AB=12 , BM=5 ,∴AE=16.9 ,∴ DE=AEAD=4.9.﹣巩 固 提 高4. 如图,∠ ACB=ADC=90°∠, BC=a , AC=b ,AB=c ,要使△ ABCCAD∽△,只要 CD 等于( )A巩 固 提 高5. 把△ ABC 的各边都扩大为原来的 3 倍,得到△ A1B1C1 ,则下列结论不正确的是 ( ) A .△ ABC 与△ A1B1C1 的三边成比例 B .△ ABCA∽△1B1C1 C .△ ABC 与△ A1B1C1...