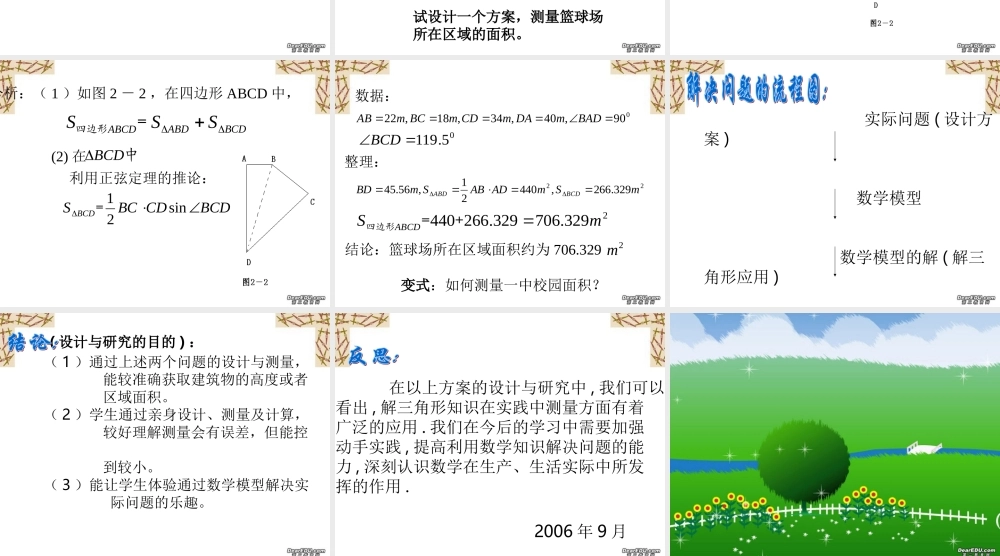
解三角形的知识本身是从人类长期的生产和生活实践中产生和发展起来的,在数学发展历史上,受到天文测量,航海测量和地理测量等方面实践活动的推动,解三角形的理论得到不断发展,并被应用于解决许多测量问题 . 试设计一种方案,测量新一栋教学楼的高度。 ( 让各组的同学提出自己的方案 ) 、测出 CD 长度。工具:测角仪,卷尺。ACD.)sin(sin CDACABCRt分析:( 1 )如图 1 - 1 ,在中,利用正弦定理求出 AC , ( 2 )中,求出 AB 。,.sin)sin(sinsinCDACAB 选点 C 、 D 两次测得仰角数据: CD=10m,0040,55 整理: AC=52.66m AB=20.345m 结论:新一栋教学楼的高度约为 20.345m. 与实际高度 20.5m 有误差 , 误差是怎么产生的呢 ?变式:如何测量神光山顶的电视塔高度?试设计一个方案,测量篮球场所在区域的面积。BCDBAD ,.工具:测角仪,卷尺。 选取篮球场所在区域的四个测量点 A 、 B 、 C 、 D ,测出: AB 、 BC 、 CD 、 AD 的长度及BCDABDABCDSSS=四边形中BCDBCDCDBCS BCDsin21=分析:( 1 )如图 2 - 2 ,在四边形 ABCD 中, (2) 在利用正弦定理的推论:090,40,34,18,22BADmDAmCDmBCmAB05.119BCD数据: 22329.266,44021,56.45mSmADABSmBDBCDABD2329.706329.266440mSABCD+=四边形整理: 变式:如何测量一中校园面积?结论:篮球场所在区域面积约为 706.3292m 实际问题 ( 设计方案 ) 数学模型 数学模型的解 ( 解三角形应用 ) 实际问题的解 ( 1 )通过上述两个问题的设计与测量, 能较准确获取建筑物的高度或者 区域面积。 ( 2 )学生通过亲身设计、测量及计算, 较好理解测量会有误差,但能控制 到较小。 ( 3 )能让学生体验通过数学模型解决实 际问题的乐趣。 ( 设计与研究的目的 ) : 在以上方案的设计与研究中 , 我们可以看出 , 解三角形知识在实践中测量方面有着广泛的应用 . 我们在今后的学习中需要加强动手实践 , 提高利用数学知识解决问题的能力 , 深刻认识数学在生产、生活实际中所发挥的作用 .2006 年 9 月