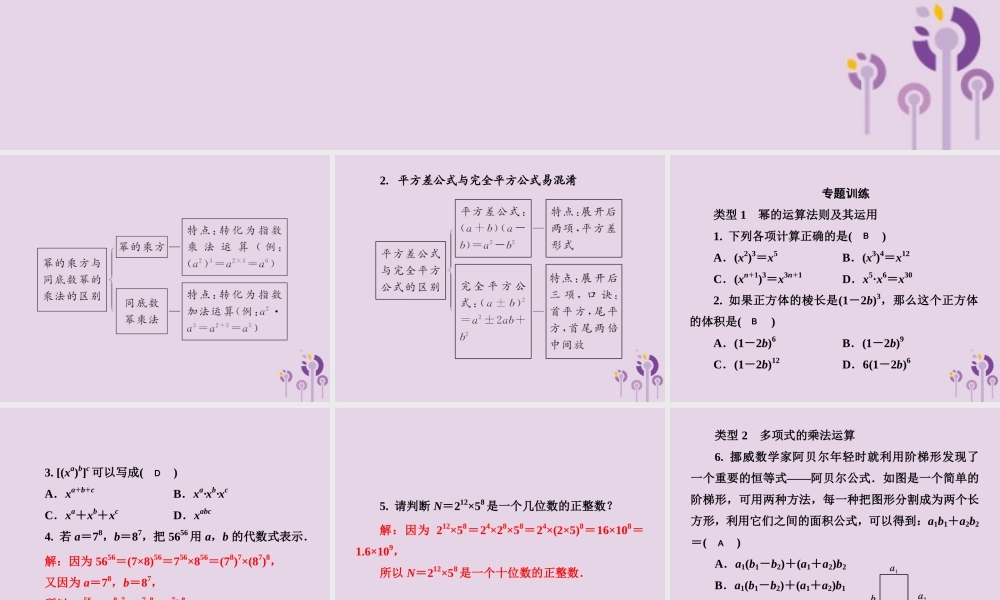
微专题 4 整式的乘法及其应用2.平方差公式与完全平方公式易混淆 专题训练 类型 1 幂的运算法则及其运用 1. 下列各项计算正确的是( ) A.(x2)3=x5 B.(x3)4=x12 C.(xn+1)3=x3n+1 D.x5·x6=x30 2. 如果正方体的棱长是(1-2b)3,那么这个正方体的体积是( ) A.(1-2b)6 B.(1-2b)9 C.(1-2b)12 D.6(1-2b)6 B B 3. [(xa)b]c 可以写成( ) A.xa+b+c B.xa·xb·xc C.xa+xb+xc D.xabc 4. 若 a=78,b=87,把 5656 用 a,b 的代数式表示. 解:因为 5656=(7×8)56=756×856=(78)7×(87)8, 又因为 a=78,b=87, 所以 5656=(78)7×(87)8=a7b8. D 5. 请判断 N=212×58 是一个几位数的正整数? 解:因为 212×58=24×28×58=24×(2×5)8=16×108=1.6×109, 所以 N=212×58 是一个十位数的正整数. 类型 2 多项式的乘法运算 6. 挪威数学家阿贝尔年轻时就利用阶梯形发现了一个重要的恒等式——阿贝尔公式.如图是一个简单的阶梯形,可用两种方法,每一种把图形分割成为两个长方形,利用它们之间的面积公式,可以得到:a1b1+a2b2=( ) A.a1(b1-b2)+(a1+a2)b2 B.a1(b1-b2)+(a1+a2)b1 C.a2(b1-b2)+(a1+a2)b1 D.a2(b1-b2)+(a1+a2)b2 A 7. 三角形表示 3abc,方框表示-4xywz,则×=________. -36m6n3 8. 计算: (1)-9a2b·(x-y)4·13·ab2(y-x)3; 解:原式=3a3b3(x-y)7; (2)(-9a)·2a2-(-9a)·(-23a2)+9a3·(-49). 解:原式=-28a3. 类型 3 乘法公式的应用 9. 已知 78-1 可被 45 和 55 之间的两个数整除,这两个数是( ) A.47,48 B.45,47 C.50,48 D.46,47 10. 计算100022522-2482的结果是( ) A.12 B.1000 C.500 D.2000 C C 11. 若实数 x,y,z 满足(x-z)2-4(x-y)(y-z)=0,则下列式子一定成立的是( ) A.x+y+z=0 B.x+y-2z=0 C.y+z-2x=0 D.x+z-2y=0 【解析】因为(x-z)2-4(x-y)(y-z)=0.所以 x2+z2-2xz-4xy+4xz+4y2-4yz=0,所以 x2+z2+2xz-4xy+4y2-4yz=0,所以(x+z)2-4y(x+z)+4y2=0,所以(x+z-2y)2=0,所以 x+z-2y=0. D 12. 若 a+b=5,ab=6,则(a-b)2=__. 13. 先化简,再求值:2a(a+2b)-(a+2b)2,其中 a=-1,b=-3. 解:原式=a2-4b2,当 a=-1,b=-3 时, 原式=-35. 1 类型 ...