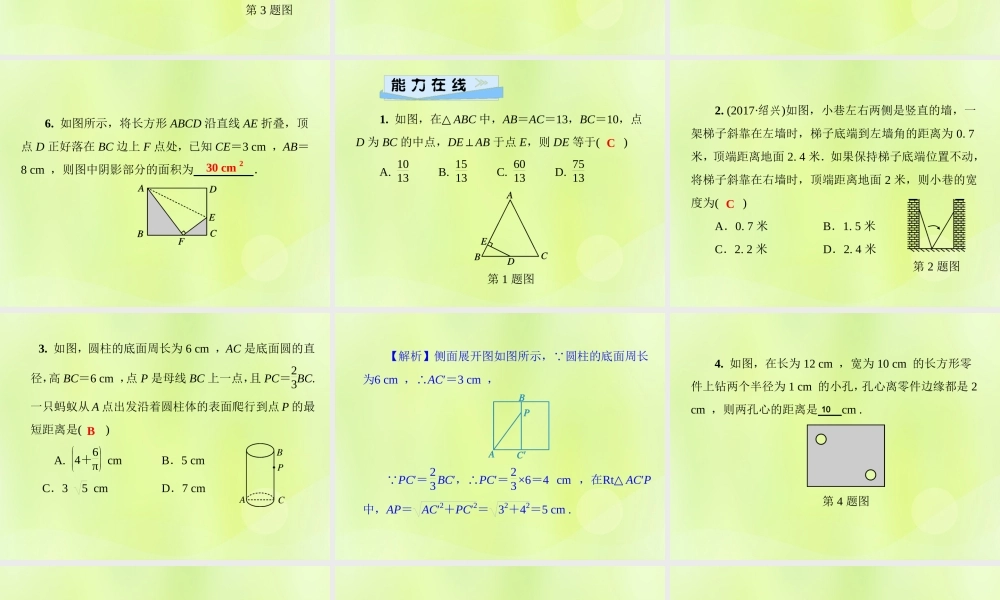
第 14 章 勾股定理14.2 勾股定理的应用第 1 课时 勾股定理的应用 1. 勾股定理的变形:若直角三角形的两直角边分别为 a、b,斜边为 c,则 a2+b2=c2 或 a2= 或b2= 或 a= 或 b= . 2. 立体图形中最短路线的求法:因为平面内,两点之间 最短,所以在立体图形中,求两点间的最短距离时,把立体图形的表面(或侧面)展开,然后再利用勾股定理来求. c2-b2 c2-a2 c2-b2 c2-a2 线段 知识点 不在同一平面上的两点之间的最短距离 1. 如图,长方体的长为 15,宽为 10,高为 20,点 B离点 C 的距离为 5,一只蚂蚁如果要沿着长方体的表面从点 A 爬到点 B,需要爬行的最短距离是( ) A.5 37 B.25 C.10 5+5 D.35 第 1 题图 B 2. 如图所示的圆柱体中,底面半径为2π,高为 2,若一只小虫从 A 点出发沿圆柱体的侧面爬行到 C 点,则小虫爬行的最短路径为 .(结果保留根号) 第 2 题图 2 2 知识点 化归与建立直角三角形模型解决实际问题 3. 如图所示,木工做一个长 80 厘米,宽 60 厘米的长方形木框,需在对角的顶点钉一个加固木条,则木条的长为( ) A.90 厘米 B.100 厘米 C.150 厘米 D.110 厘米 第 3 题图 B 4. 一架 25 分米长的梯子,斜立在一竖直的墙上,这时梯足距离墙底端 7 分米.如果梯子的顶端沿墙下滑4 分米,那么梯足将滑动( ) A.9 分米 B.15 分米 C.5 分米 D.8 分米 D 5. 已知,如图所示,△ ABC 中,AC=6,AB=BC=5,则 BC 边上的高 AD= . 第 5 题图 245 6. 如图所示,将长方形 ABCD 沿直线 AE 折叠,顶点 D 正好落在 BC 边上 F 点处,已知 CE=3 cm ,AB=8 cm ,则图中阴影部分的面积为 . 30 cm 2 1. 如图,在△ ABC 中,AB=AC=13,BC=10,点D 为 BC 的中点,DE⊥AB 于点 E,则 DE 等于( ) A. 1013 B. 1513 C. 6013 D. 7513 第 1 题图 C 2. (2017·绍兴)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为 0. 7米,顶端距离地面 2. 4 米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面 2 米,则小巷的宽度为( ) A.0. 7 米 B.1. 5 米 C.2. 2 米 D.2. 4 米 第 2 题图 C 3. 如图,圆柱的底面周长为 6 cm ,AC 是底面圆的直径,高 BC=6 cm ,点 P 是母线 BC 上一...