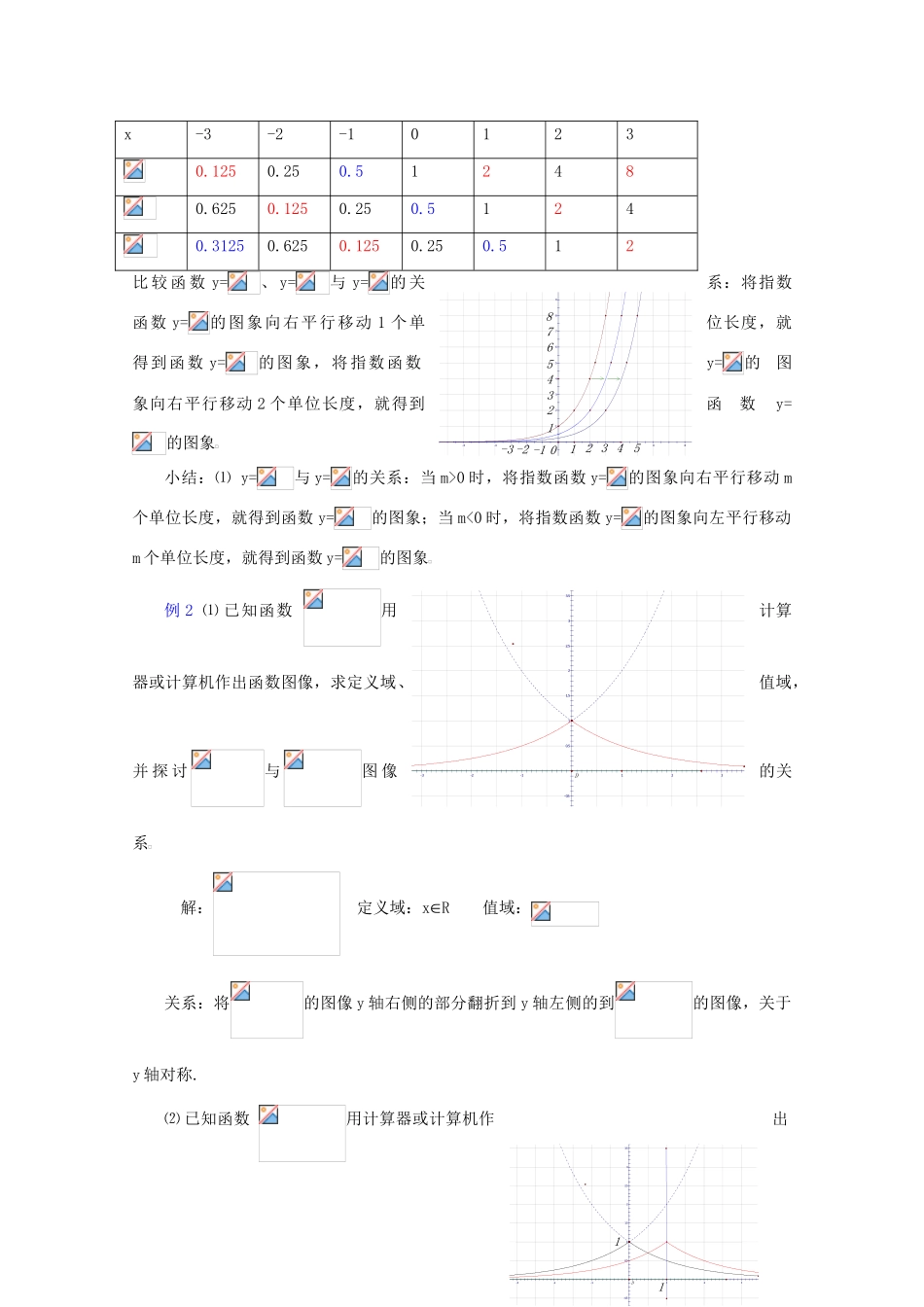
课 题:2.6.3 指数函数 3教学目的: 1.了解函数图象的变换;能运用指数函数的图象和性质解决一些简单问题.2.培养培养观察分析、抽象概括能力、归纳总结能力、逻辑推理能力;3.培养发现问题和提出问题的意识、善于独立思考的习惯 教学重点:函数图象的变换;指数函数性质的运用教学难点:函数图象的变换;指数函数性质的运用.授课类型:新授课课时安排:1 课时教 具:多媒体、实物投影仪教学过程:一、复习引入:指数函数的定义、图像、性质(定义域、值域、单调性)二、新授内容:例 1(课本第 82 页 例 2)用计算机作出的图像,并在同一坐标系下作出下列函数的图象,并指出它们与指数函数 y=的图象的关系,⑴y=与 y=. ⑵y=与 y=.解:⑴作出图像,显示出函数数据表x-3-2-101230.1250.250.512480.250.51248160.512481632比 较 函 数 y=、 y=与 y=的关 系 :将指数函数 y=的图象向左平行移动 1个 单 位长度,就得到函数 y=的图象,将指数 函 数y=的图象向左平行移动 2 个单位长度,就 得 到函数 y=的图象⑵ 作出图像,显示出函数数据表987654321-6-4-2246887654321-3 -20-13213.532.521.510.5-0.5-3-2-112311Dx-3-2-101230.1250.250.512480.6250.1250.250.51240.31250.6250.1250.250.512比 较 函 数 y=、 y=与 y=的 关系:将指数函数 y=的图象向右平行移动 1 个单位长度,就得到函数 y=的图象,将指数函数y=的图象向右平行移动 2 个单位长度,就得到函数y=的图象小结:⑴ y=与 y=的关系:当 m>0 时,将指数函数 y=的图象向右平行移动 m个单位长度,就得到函数 y=的图象;当 m<0 时,将指数函数 y=的图象向左平行移动m 个单位长度,就得到函数 y=的图象例 2 ⑴ 已知函数 用计算器或计算机作出函数图像,求定义域、值域,并 探 讨与图 像的关系 解: 定义域:xR 值域: 关系:将的图像 y 轴右侧的部分翻折到 y 轴左侧的到的图像,关于y 轴对称.⑵ 已知函数 用计算器或计算机作出987654321-6-4-224685487654321-3 -20-13213.532.521.510.5-0.5-3-2-1123D函数图像,求定义域、值域,并探讨与图像的关系解: 定义域:xR 值域:关系:将(x>1)的图像在直线 x=1 右侧的部分翻折到直线 x=1 左侧得到的图像,是关于直线 x=1 对称⑵ 推广:对于有些复合函数的图象,则常用基本函数图象+变换方法作出:基本函数图象+变换:即把我们熟知的基本函数图象,通...