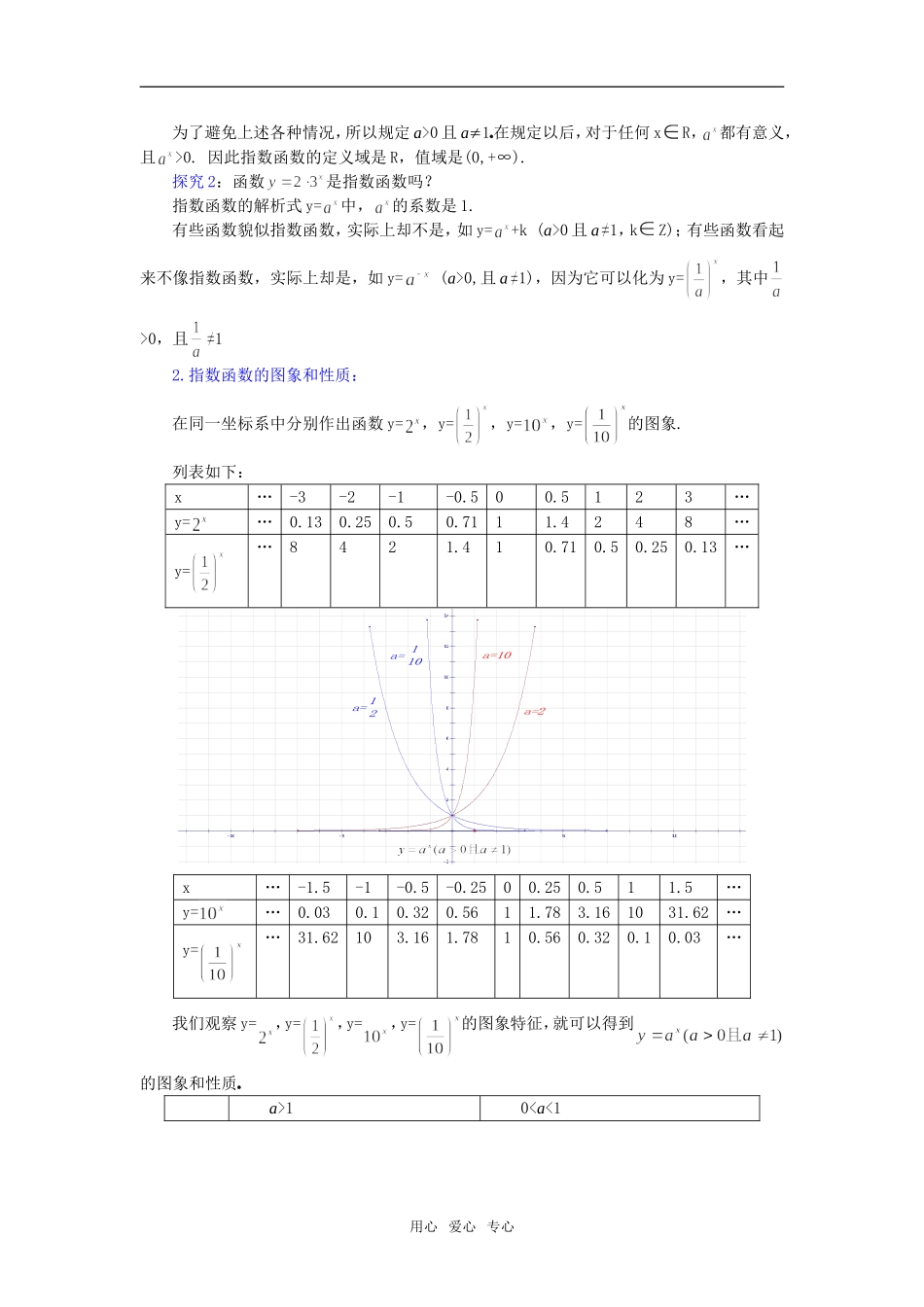
2.2.2 指数函数第一课时三维目标1.知识与技能了解指数函数模型的实际背景,理解指数函数的概念和意义,掌握数形结合研究指数性质的方法和能力。2.过程与方法通过绘制指数函数的图像体验指数函数性质的形成过程,并学会由数及形、由形及数研究函数的方法。3.情感、态度与价值观通过解决简单实际问题的过程,体会指数函数是一种重要的函数模型,激发学生的学习兴趣,培养创新意识。重点难点1.教学重点:指数函数的图象、性质奎屯王新敞新疆2.教学难点:指数函数的图象性质与底数 a 的关系.教学过程一、复习引入:引例 1:某种细胞分裂时,由 1 个分裂成 2 个,2 个分裂成 4 个,……. 1 个这样的细胞分裂 x 次后,得到的细胞个数 y 与 x 的函数关系是什么?分裂次数:1,2,3,4,…,x细胞个数:2,4,8,16,…,y由上面的对应关系可知,函数关系是.引例 2:某种商品的价格从今年起每年降低 15%,设原来的价格为 1,x 年后的价格为 y,则 y 与 x 的函数关系式为 奎屯王新敞新疆在,中指数 x 是自变量,底数是一个大于 0 且不等于 1 的常量.我们把这种自变量在指数位置上而底数是一个大于 0 且不等于 1 的常量的函数叫做指数函数.二、新授内容:1.指数函数的定义:函数叫做指数函数,其中 x 是自变量,函数定义域是 R奎屯王新敞新疆探究 1:为什么要规定 a>0,且 a 1 呢?① 若 a=0,则当 x>0 时,=0;当 x 0 时,无意义. ② 若 a<0,则对于 x 的某些数值,可使无意义. 如,这时对于 x=,x=,…等等,在实数范围内函数值不存在.③ 若 a=1,则对于任何 xR,=1,是一个常量,没有研究的必要性. 用心 爱心 专心为了避免上述各种情况,所以规定 a>0 且 a1奎屯王新敞新疆在规定以后,对于任何 xR, 都有意义,且>0. 因此指数函数的定义域是 R,值域是(0,+∞).探究 2:函数是指数函数吗?指数函数的解析式 y=中,的系数是 1.有些函数貌似指数函数,实际上却不是,如 y=+k (a>0 且 a 1,kZ);有些函数看起来不像指数函数,实际上却是,如 y= (a>0,且 a 1),因为它可以化为 y=,其中>0,且12.指数函数的图象和性质:在同一坐标系中分别作出函数 y=,y=,y=,y=的图象.列表如下:x…-3-2-1-0.500.5123…y=…0.130.250.50.7111.4248…y=…8421.410.710.50.250.13…1412108642-2-10-5510a= 110a=10a= 12a=2x…-1.5-1-0.5-0.2500.250.511.5…y=…0.030.10.320...