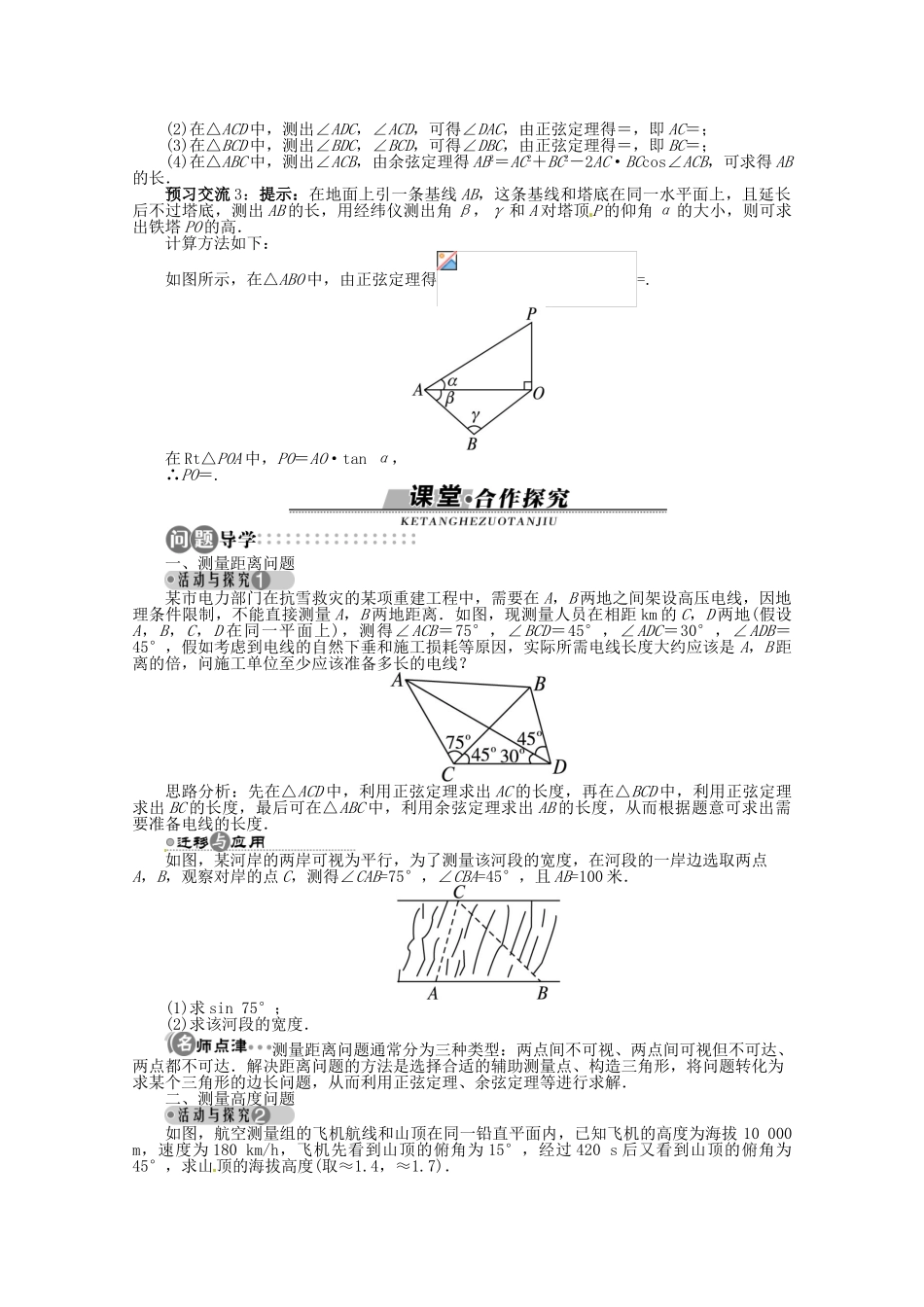
8.3 解三角形的应用举例第 1 课时 距离与高度问题学习目标重点难点1.知道仰角、俯角等概念;2.会用正余弦定理解决距离计算问题;3.会用正余弦定理解决高度计算问题.重点:距离与高度问题的求解;难点:正余弦定理的选择与运用.1.仰角与俯角如下图,当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫作________,视线在水平线下方的角叫作________.预习交流 1假若由较低的 A 点望较高的 B 点时,仰角为 α,而由 B 点望 A 点时,俯角为 β,那么 α与 β 有何关系?2.测量距离问题预习交流 2如何测量地面上两个不能到达的地方之间的距离?例如:A,B 两地在河的一边,怎样测出 A,B 间距离?3.测量高度问题预习交流 3怎样测量一个底部不能到达的建筑物的高度?例如:要测量某铁塔 PO 的高度,但不能到达铁塔的底部,在只能使用简单的测量工具的前提下,你能设计出哪些测量方法?并提供计算方法.在预习中还有哪些问题需要你在听课时加以关注?请在下列表格中做个备忘吧!我的学困点我的学疑点答案:1.仰角 俯角预习交流 1:提示:必有 α=β.预习交流 2:提示:方法步骤如下:(1)先在河对岸上选 C 地,D 地,并量出 DC 的长度;(2)在△ACD 中,测出∠ADC,∠ACD,可得∠DAC,由正弦定理得=,即 AC=;(3)在△BCD 中,测出∠BDC,∠BCD,可得∠DBC,由正弦定理得=,即 BC=;(4)在△ABC 中,测出∠ACB,由余弦定理得 AB2=AC2+BC2-2AC·BCcos∠ACB,可求得 AB的长.预习交流 3:提示:在地面上引一条基线 AB,这条基线和塔底在同一水平面上,且延长后不过塔底,测出 AB 的长,用经纬仪测出角 β,γ 和 A 对塔顶 P 的仰角 α 的大小,则可求出铁塔 PO 的高.计算方法如下:如图所示,在△ABO 中,由正弦定理得=.在 Rt△POA 中,PO=AO·tan α,∴PO=.一、测量距离问题某市电力部门在抗雪救灾的某项重建工程中,需要在 A,B 两地之间架设高压电线,因地理条件限制,不能直接测量 A,B 两地距离.如图,现测量人员在相距 km 的 C,D 两地(假设A,B,C,D 在同一平面上),测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,假如考虑到电线的自然下垂和施工损耗等原因,实际所需电线长度大约应该是 A,B 距离的倍,问施工单位至少应该准备多长的电线?思路分析:先在△ACD 中,利用正弦定理求出 AC 的长度,再在△BCD 中,利用正...