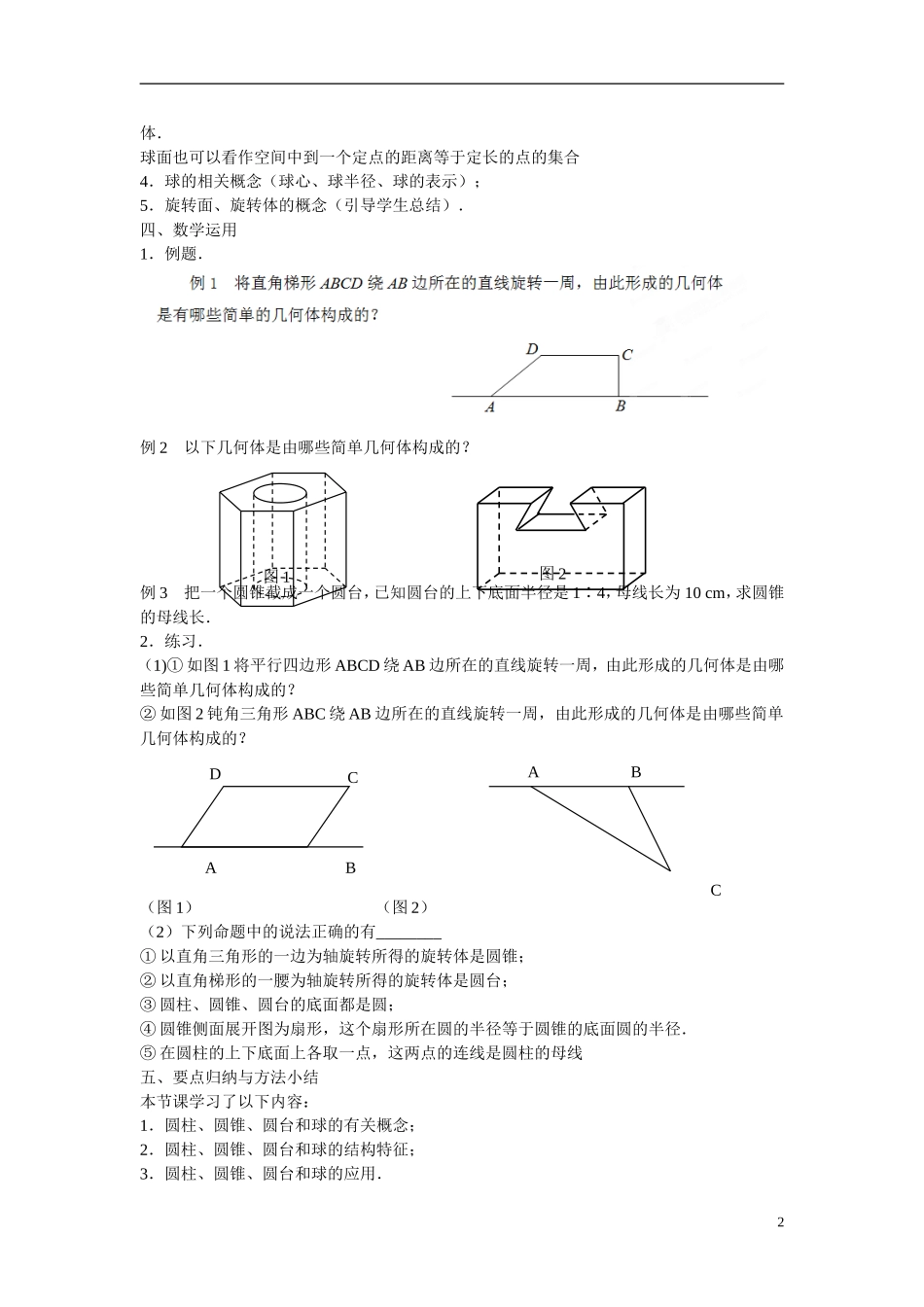
江苏省苏州市第五中学高中数学 1.1.2 圆柱、圆锥、圆台和球教案 苏教版必修 2教学目标:1.能根据几何结构特征理解空间旋转体形成过程;2.认识圆柱、圆锥、圆台和球的结构特征;3.掌握圆柱、圆锥、圆台和球的截面及它们之间的关系.教材分析及教材内容的定位:教材先让学生思考圆柱、圆锥、圆台、球的生成规律,然后给出它们的定义,让学生初步理解“旋转体”的概念.教学中可结合实物模型或计算机演、圆锥、圆台、球的生成过程,引导学生思考圆柱、圆锥、圆台、球的结构特征;也可以类比棱柱、棱锥、棱台的生成过程认识圆柱、圆锥、圆台的结构特征;类比圆的定义得出球面的定义.教学重点:让学生感受大量空间实物及模型、概括出圆柱、圆锥、圆台和球的概念.教学难点:难点是区分一个旋转体由哪些基本几何体构成.教学方法:观察、发现、探究.教学过程:一、问题情境1.复习棱柱、棱锥、棱台的有关概念.小结:移——缩——截.2.旋转会产生什么样的结果呢?仔细观察下面的几何体,它们有什么共同特点或生成规律? 二、学生活动通过观察、思考、交流、讨论得出结论.三、建构数学圆柱、圆锥、圆台的概念;2.圆柱、圆锥、圆台的相关概念(轴、高、底面、母线);思考:圆柱、圆锥、圆台之间有何关系?(引导学生从概念的形成和结构特征来分析三者之间的关系)3.球面及球的概念;半圆绕着它的直径所在的直线旋转一周而形成的曲面叫做球面,球面围成的几何体叫做球1体.球面也可以看作空间中到一个定点的距离等于定长的点的集合 4.球的相关概念(球心、球半径、球的表示);5.旋转面、旋转体的概念(引导学生总结).四、数学运用1.例题.例 2 以下几何体是由哪些简单几何体构成的?例 3 把一个圆锥截成一个圆台,已知圆台的上下底面半径是 1∶4,母线长为 10 cm,求圆锥的母线长.2.练习.(1)① 如图 1 将平行四边形 ABCD 绕 AB 边所在的直线旋转一周,由此形成的几何体是由哪些简单几何体构成的?② 如图 2 钝角三角形 ABC 绕 AB 边所在的直线旋转一周,由此形成的几何体是由哪些简单几何体构成的?(图 1) (图 2)(2)下列命题中的说法正确的有________① 以直角三角形的一边为轴旋转所得的旋转体是圆锥;② 以直角梯形的一腰为轴旋转所得的旋转体是圆台;③ 圆柱、圆锥、圆台的底面都是圆;④ 圆锥侧面展开图为扇形,这个扇形所在圆的半径等于圆锥的底面圆的半径.⑤ 在圆柱的上下底面上各取...