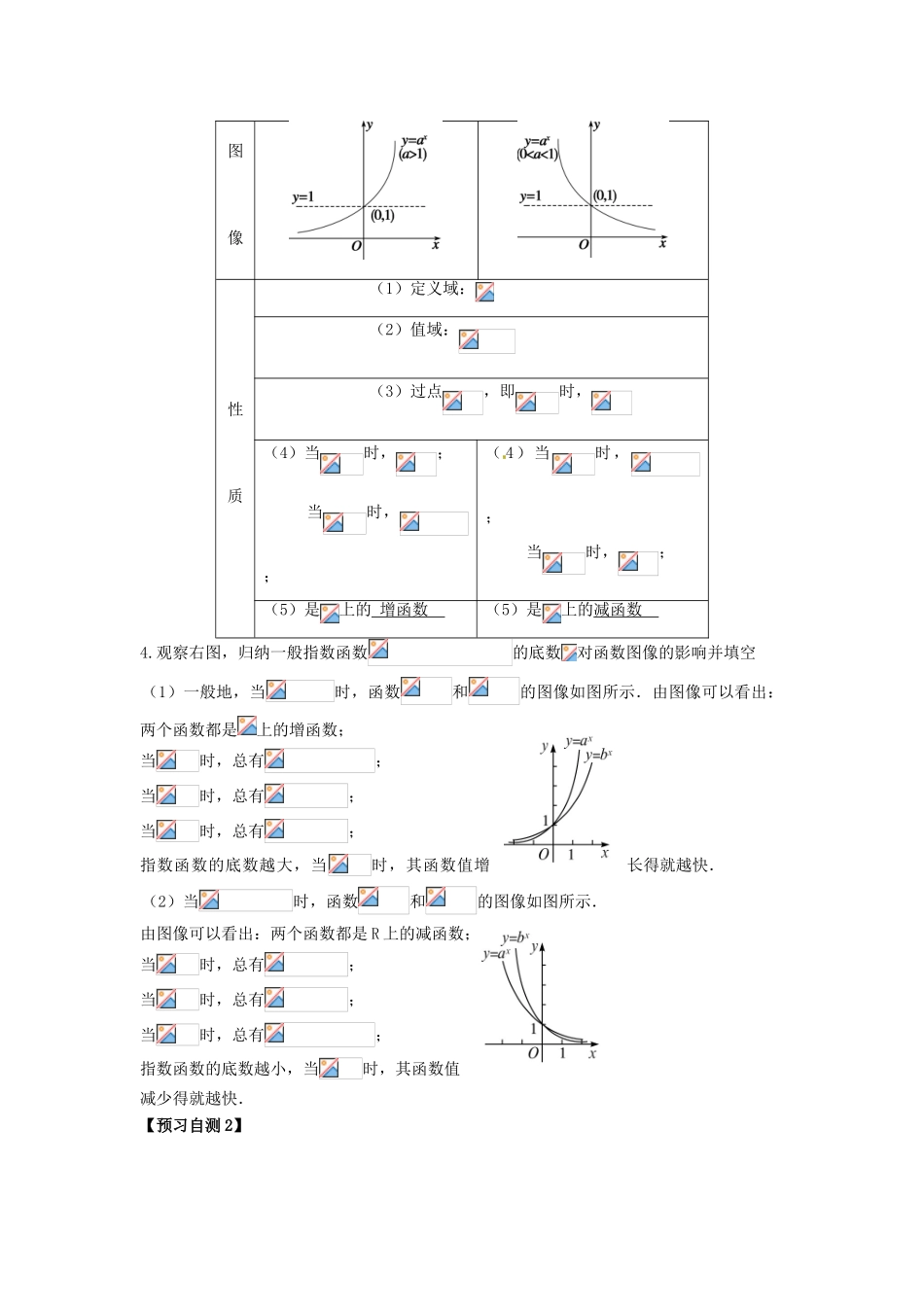
江西省宜春中学高中数学 3.2.1 指数函数导学案 新人教版必修 1一、课前自主导学【学习目标】(1)在实数指数幂的基础上,理解指数函数的概念,能画出具体指数函数的图像;(2)在理解指数函数概念的前提下,能判断一个函数是否为指数函数;(3)通过四个底数不同的指数函数归纳指数函数的基本性质,并能比较两个值的大小,求解简单的不等式.【重点、难点】指数函数的概念、图像及性质;比较两个值大小.【教材助读 1】认真阅读课本 P70,理解指数函数的定义并填空1.指数函数的定义:函数叫做 指数函数 ,其中自变量出现在指数的位置上.【预习自测 1】1.函数和函数有什么区别?解:函数的指数是变量,是指数函数;函数的指数是常数,是幂函数.2.在下列的关系式中,哪些不是指数函数,为什么?(1);(2);(3);(4);(5);(6)且;(7).解:只有(4),(6)是指数函数,因它们满足指数函数的定义;(1)中解析式可变形为,不满足指数函数的形式;(2)中底数为负,所以不是;(3)中解析式多一负号,所以不是,(5)中指数为常数,所以不是;(6)中令,则且,所以是指数函数.(7)中底数是变量,不是常数.【教材助读 2】1.请同学们在同一直角坐标中作出函数 的图像.2.根据上述所作图像填写下表函数 图像性质共同点定义域:;值域:;过点,即时,不同点,是上的增函数,是上的减函数比更靠近于轴和轴比更靠近于轴和轴与关于轴对称,与关于轴对称3.从上述图像,可归纳一般指数函数的图像和性质,填写下表图像性质(1)定义域: (2)值域:(3)过点,即时, (4)当时,; 当时,;( 4)当时,; 当时,;(5)是上的 增函数 (5)是上的减函数 4.观察右图,归纳一般指数函数的底数对函数图像的影响并填空(1)一般地,当时,函数和的图像如图所示.由图像可以看出:两个函数都是上的增函数;当时,总有;当时,总有;当时,总有;指数函数的底数越大,当时,其函数值增长得就越快.(2)当时,函数和的图像如图所示.由图像可以看出:两个函数都是 R 上的减函数;当时,总有;当时,总有;当时,总有; 指数函数的底数越小,当时,其函数值减少得就越快.【预习自测 2】1.关于指数函数和的图像,下列说法不正确的是( B )A.它们的图像都过点,并且都在轴的上方.B.它们的图像关于轴对称,因此它们是偶函数.C.它们的定义域都是,值域都是.D.自左向右看的图像是上升的,的图像是下降的.2.函数在上是减函数,则的取值范围是( D )A...