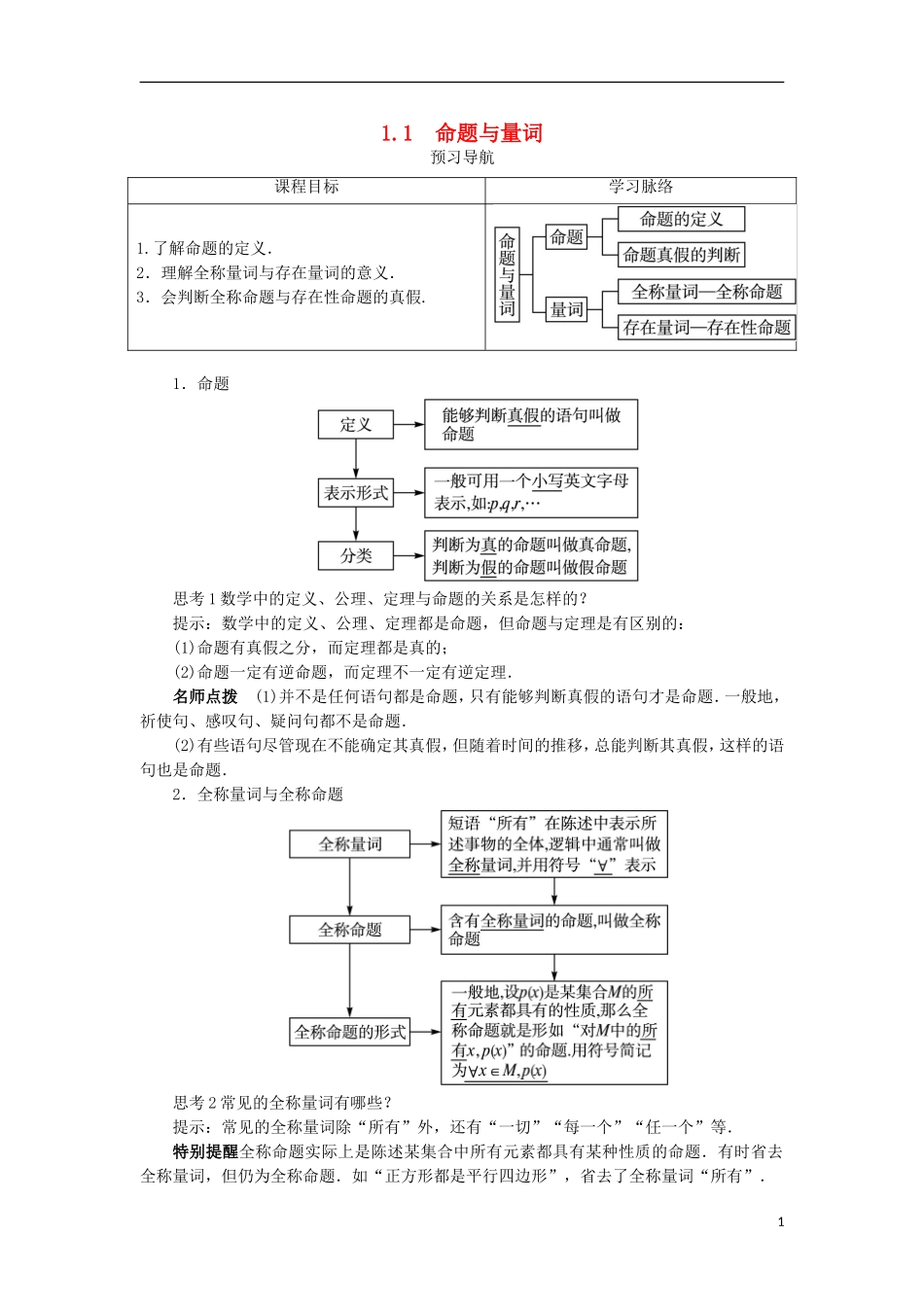
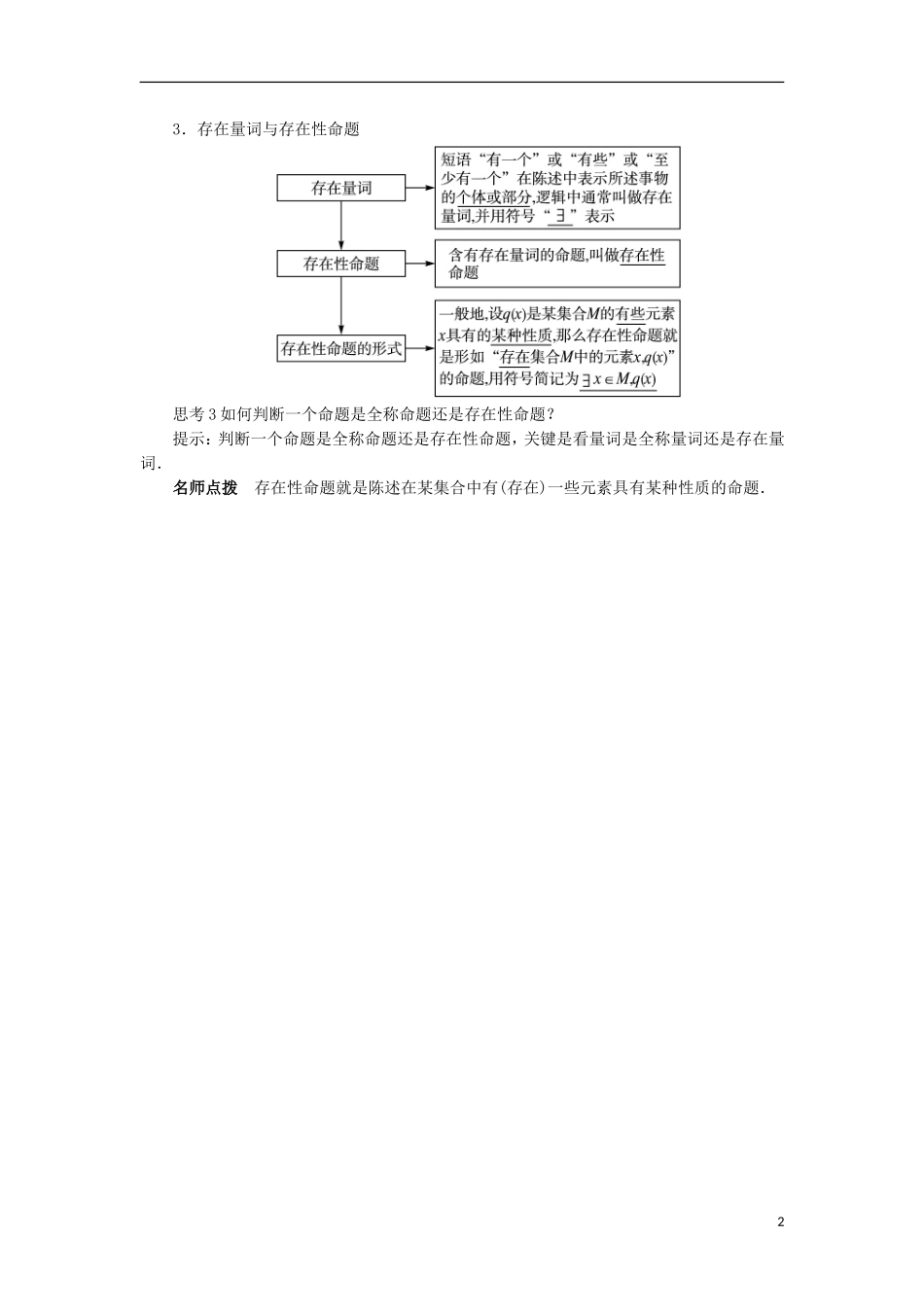
1.1 命题与量词预习导航课程目标学习脉络1.了解命题的定义.2.理解全称量词与存在量词的意义.3.会判断全称命题与存在性命题的真假.1.命题思考 1 数学中的定义、公理、定理与命题的关系是怎样的?提示:数学中的定义、公理、定理都是命题,但命题与定理是有区别的:(1)命题有真假之分,而定理都是真的;(2)命题一定有逆命题,而定理不一定有逆定理.名师点拨 (1)并不是任何语句都是命题,只有能够判断真假的语句才是命题.一般地,祈使句、感叹句、疑问句都不是命题.(2)有些语句尽管现在不能确定其真假,但随着时间的推移,总能判断其真假,这样的语句也是命题.2.全称量词与全称命题思考 2 常见的全称量词有哪些?提示:常见的全称量词除“所有”外,还有“一切”“每一个”“任一个”等.特别提醒全称命题实际上是陈述某集合中所有元素都具有某种性质的命题.有时省去全称量词,但仍为全称命题.如“正方形都是平行四边形”,省去了全称量词“所有”.13.存在量词与存在性命题思考 3 如何判断一个命题是全称命题还是存在性命题?提示:判断一个命题是全称命题还是存在性命题,关键是看量词是全称量词还是存在量词.名师点拨 存在性命题就是陈述在某集合中有(存在)一些元素具有某种性质的命题.2