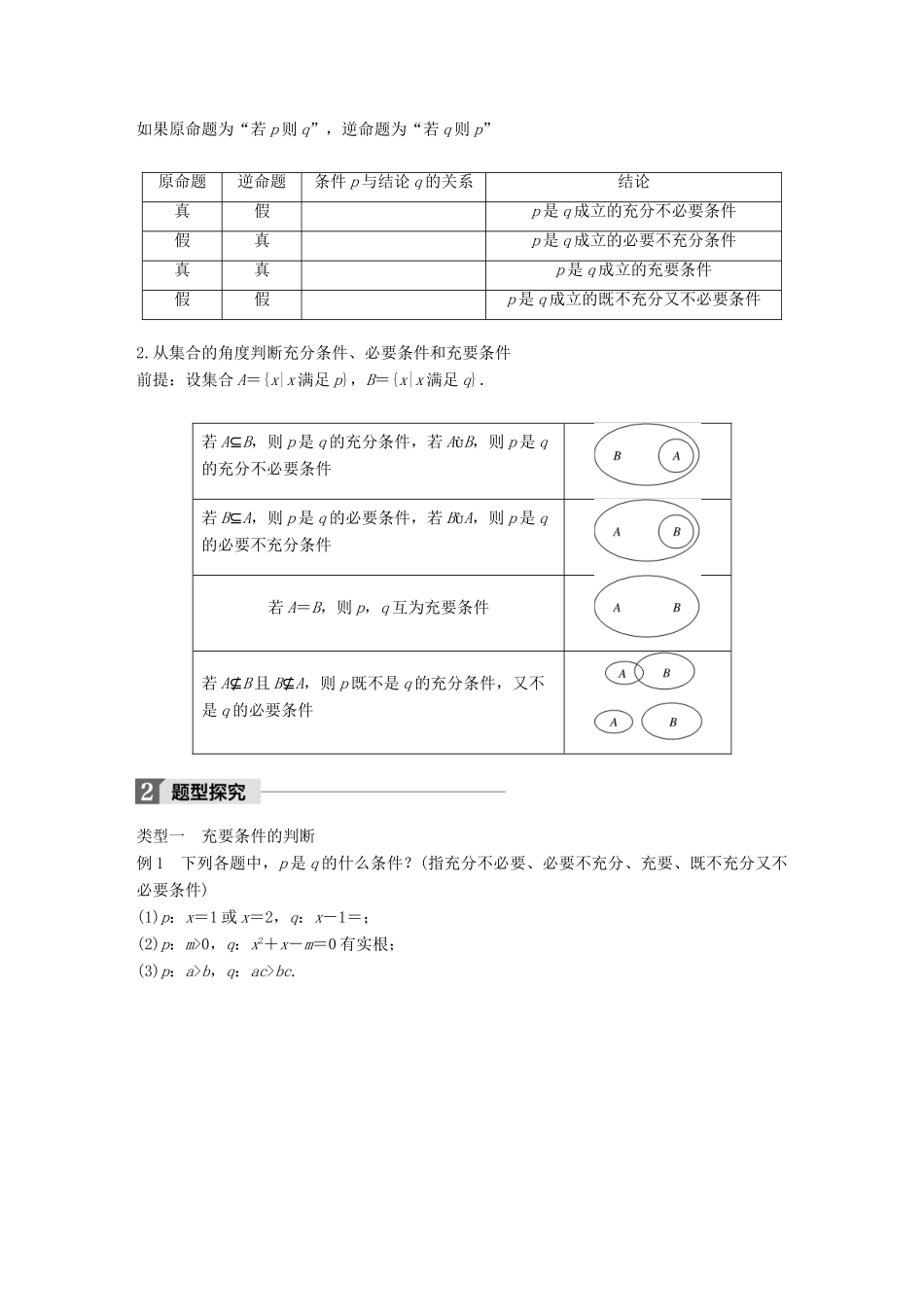
1.1.2 充分条件和必要条件学习目标 1.理解充分条件、必要条件的意义.2.会判断、证明充要条件.3.通过学习,明白对条件的判断应归结为判断命题的真假.知识点一 充分条件与必要条件的概念给出下列命题:(1)若 x>a2+b2,则 x>2ab;(2)若 ab=0,则 a=0.思考 1 你能判断这两个命题的真假吗? 思考 2 命题(1)中条件和结论有什么关系?命题(2)中呢? 梳理 命题真假“若 p 则 q”为真命题“若 p 则 q”为假命题推出关系p____qp ____q条件关系p 是 q 的______条件q 是 p 的______条件p 不是 q 的______条件q 不是 p 的______条件知识点二 充要条件的概念思考 1 命题“若整数 a 是 6 的倍数,则整数 a 是 2 和 3 的倍数”中的条件和结论有什么关系?它的逆命题成立吗? 思考 2 若设 p:整数 a 是 6 的倍数,q:整数 a 是 2 和 3 的倍数,则 p 是 q 的什么条件?q 是p 的什么条件?梳理 一般地,如果既有 p⇒q,又有 q⇒p,就记作________.此时,我们说,p 是 q 的________________,简称充要条件.知识点三 常见的四种条件1.从命题的真假判断充分条件、必要条件和充要条件如果原命题为“若 p 则 q”,逆命题为“若 q 则 p”原命题逆命题条件 p 与结论 q 的关系结论真假p 是 q 成立的充分不必要条件假真p 是 q 成立的必要不充分条件真真p 是 q 成立的充要条件假假p 是 q 成立的既不充分又不必要条件2.从集合的角度判断充分条件、必要条件和充要条件前提:设集合 A={x|x 满足 p},B={x|x 满足 q}.若 A⊆B,则 p 是 q 的充分条件,若 AB,则 p 是 q的充分不必要条件若 B⊆A,则 p 是 q 的必要条件,若 BA,则 p 是 q的必要不充分条件若 A=B,则 p,q 互为充要条件若 A⊈B 且 B⊈A,则 p 既不是 q 的充分条件,又不是 q 的必要条件类型一 充要条件的判断例 1 下列各题中,p 是 q 的什么条件?(指充分不必要、必要不充分、充要、既不充分又不必要条件)(1)p:x=1 或 x=2,q:x-1=;(2)p:m>0,q:x2+x-m=0 有实根;(3)p:a>b,q:ac>bc. 反思与感悟 充分条件、必要条件的判断方法(1)定义法:①确定谁是条件,谁是结论.② 尝试从条件推结论,若条件能推出结论,则条件为充分条件,否则就不是充分条件.③ 尝试从结论推条件,若结论能推出条件,则条件为必要条件,否则就不是必要条件.(2)...