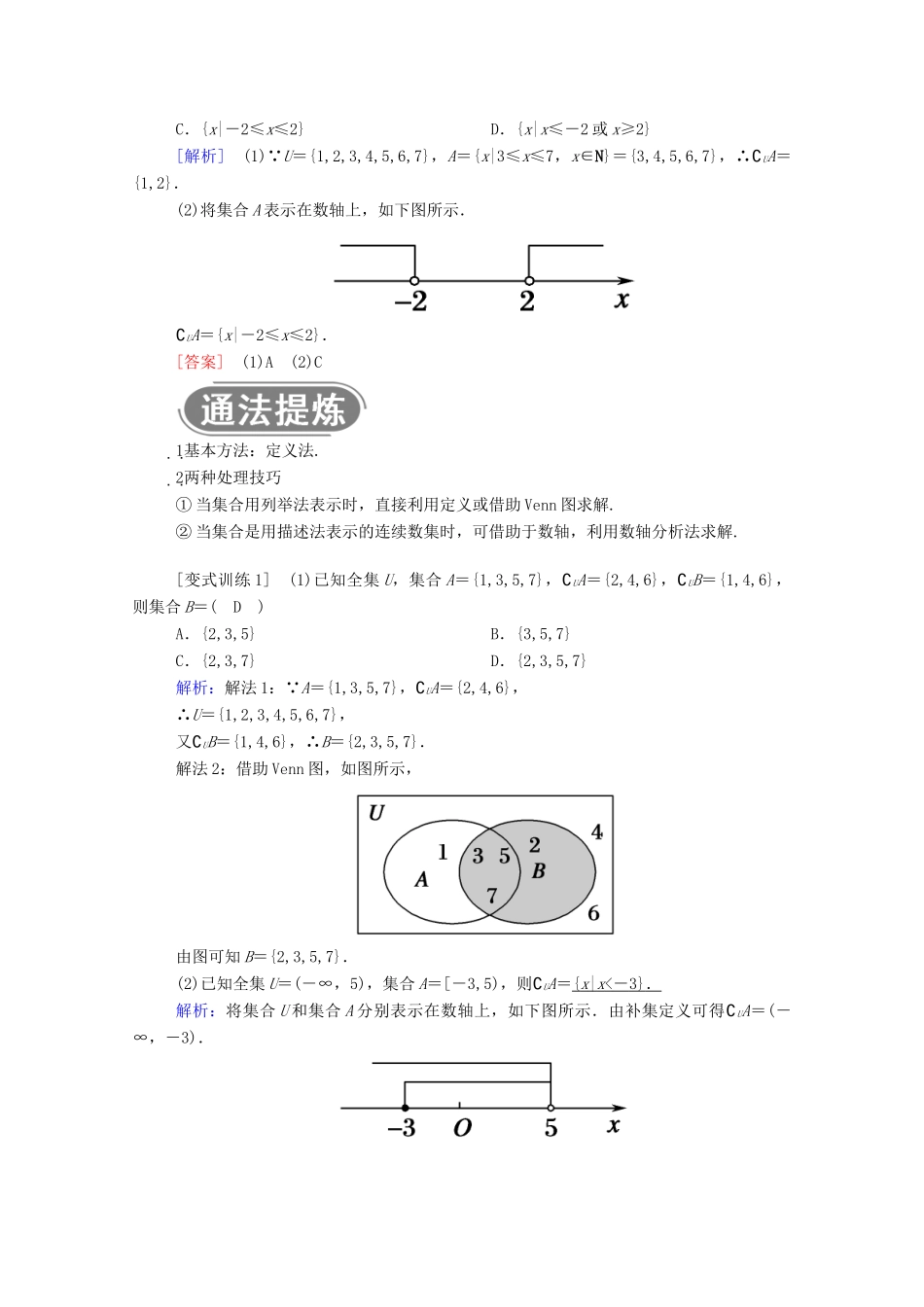
第 2 课时 全集与补集[课程目标] 1.在具体情境中,了解补集和全集的含义;2.理解在给定集合中一个子集的补集的含义,会求给定子集的补集;3.理解补集思想在解题中的应用;4.掌握集合交集、并集、补集的综合运算.知识点 补集 [填一填]1.全集的定义在研究集合与集合之间的关系时,如果所要研究的集合都是某一给定集合的 子集,那么称这个给定的集合为全集,通常用 U 表示.2.补集的定义如果给定集合 A 是全集 U 的一个子集,则由 U 中不属于 A 的所有元素组成的集合,叫做A 在 U 中的补集,记作:∁UA,读作“A 在 U 中的补集 ”,即∁UA={x|x∈U,且 x∉A}.3.补集与全集的性质(1)∁U(∁UA)=A;(2)A∪(∁UA)=U;(3)A∩(∁UA)=∅.[答一答]1.用 Venn 图如何表示 A 在 U 中的补集?提示:如图阴影部分.2.研究某个集合的补集时,该集合和全集之间是什么关系?提示:该集合必须是全集的一个子集.3.全集包含任何一个元素吗?∁AC 与∁BC 相等吗?提示:全集仅包含我们研究问题所涉及的全部元素,而非任何元素.不一定.若 A=B,则∁AC=∁BC,否则不相等.类型一 集合的补集运算 [例 1] (1)已知全集 U={1,2,3,4,5,6,7},集合 A={x|3≤x≤7,x∈N},则∁UA=( )A.{1,2} B.{3,4,5,6,7}C.{1,3,4,7} D.{1,4,7}(2)已知 U=R,集合 A={x|x<-2 或 x>2},则∁UA=( )A.{x|-22}C.{x|-2≤x≤2} D.{x|x≤-2 或 x≥2}[解析] (1) U={1,2,3,4,5,6,7},A={x|3≤x≤7,x∈N}={3,4,5,6,7},∴∁UA={1,2}.(2)将集合 A 表示在数轴上,如下图所示.∁UA={x|-2≤x≤2}.[答案] (1)A (2)C1 基本方法:定义法.2 两种处理技巧① 当集合用列举法表示时,直接利用定义或借助 Venn 图求解.② 当集合是用描述法表示的连续数集时,可借助于数轴,利用数轴分析法求解.[变式训练 1] (1)已知全集 U,集合 A={1,3,5,7},∁UA={2,4,6},∁UB={1,4,6},则集合 B=( D )A.{2,3,5} B.{3,5,7}C.{2,3,7} D.{2,3,5,7}解析:解法 1: A={1,3,5,7},∁UA={2,4,6},∴U={1,2,3,4,5,6,7},又∁UB={1,4,6},∴B={2,3,5,7}.解法 2:借助 Venn 图,如图所示,由图可知 B={2,3,5,7}.(2)已知全集 U=(-∞,5),集合 A=[-3,5),则∁UA={ x | x < - 3} . 解析:将集合 U 和集合 A 分别表示在数轴上,如下图所示.由...