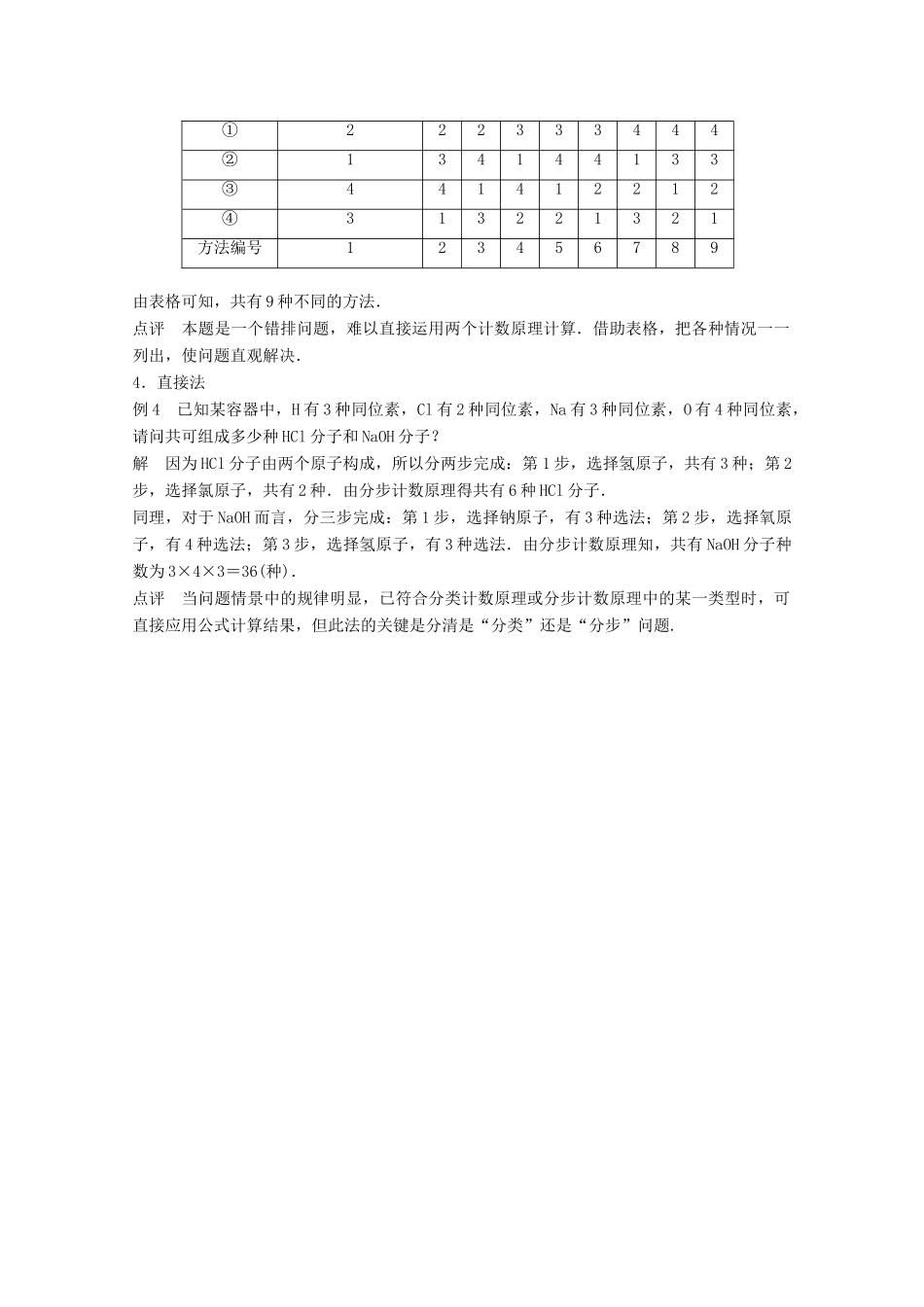
第一章 计数原理1 两个计数原理的灵活应用计数问题是数学中的重要研究对象,除了分类计数原理和分步计数原理的理论支持,对于较复杂的计数问题要针对其问题特点,灵活的运用列举法、列表法、树形图法等方法来帮助解决,使问题的解决更加实用、直观.下面通过典例来说明.1.列举法例 1 某公司电脑采购员计划用不超过 300 元的资金购买单价分别为 20 元、40 元的鼠标和键盘,根据需要,鼠标至少买 5 个,键盘至少买 3 个,则不同的选购方式共有________种.解析 依据选购鼠标和键盘的不同个数分类列举求解.若买 5 个鼠标,则可买键盘 3、4、5 个;若买 6 个鼠标,则可买键盘 3、4 个;若买 7 个鼠标,则可买键盘 3、4 个;若买 8 个鼠标,则可买键盘 3 个;若买 9 个鼠标,则可买键盘 3 个.根据分类计数原理,不同的选购方式共有 3+2+2+1+1=9(种).答案 9点评 本题背景中的数量不少,要找出关键数字,通过恰当分类和列举可得.列举看似简单,但在解决问题中显示出其实用性,并且我们还可以通过列举的方法去寻求问题中的规律.2.树形图法例 2 甲、乙、丙三人传球,从甲开始传出,并记为第一次,经过 5 次传球,球恰好回到甲手中,则不同的传球方法的种数是________.解析 本题数字不大,可用树形图法,结果一目了然.如下图,易知不同的传球方法种数为 10.答案 10点评 应用两个计数原理时,如果涉及的问题较抽象,且数量不太多时,可以用树状结构直观体现.3.列表法例 3 四个人各写一张贺年卡,放在一起,然后每个人取一张不是自己写的贺年卡,共有多少种不同的取法?解 把四个人分别编号①、②、③、④,他们写的 4 张贺年卡的各种方法全部列举出来,如下表:四个人取贺年卡的方法①222333444②134144133③441412212④313221321方法编号123456789由表格可知,共有 9 种不同的方法.点评 本题是一个错排问题,难以直接运用两个计数原理计算.借助表格,把各种情况一一列出,使问题直观解决.4.直接法例 4 已知某容器中,H 有 3 种同位素,Cl 有 2 种同位素,Na 有 3 种同位素,O 有 4 种同位素,请问共可组成多少种 HCl 分子和 NaOH 分子?解 因为 HCl 分子由两个原子构成,所以分两步完成:第 1 步,选择氢原子,共有 3 种;第 2步,选择氯原子,共有 2 种.由分步计数原理得共有 6 种 HCl 分子.同理,对于 NaOH 而言,分三步完成:第 1 步,选...