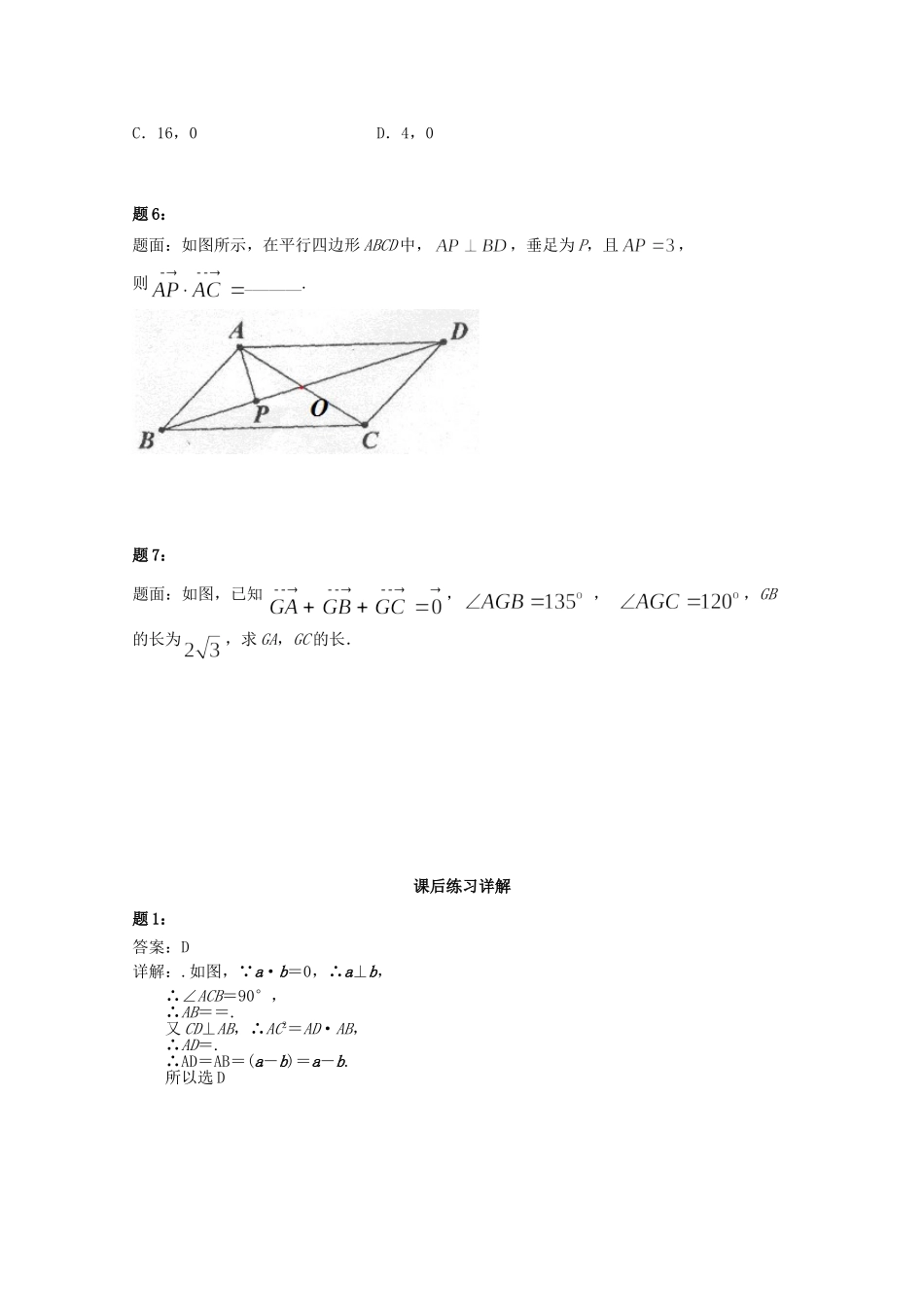
题1:题面:△ABC中,AB边的高为CD,若CB=a,CA=b,a·b=0,|a|=1,|b|=2,则AD=()A.a-bB.a-bC.a-bD.a-b题2:题面:在等腰直角三角形ABC中,D是斜边BC的中点,如果AB的长为2,则的值为________.题3:题面:若O为ABC的内心,且满足,则△ABC的形状为()A.等腰三角形B.正三角形C.直角三角形D.钝角三角形题4:题面:已知点P是△ABC的内心(三个内角平分线交点)、外心(三条边的中垂线交点)、重心(三条中线交点)、垂心(三个高的交点)之一,且满足,则点P一定是△ABC的()A.内心B.外心C.垂心D.重心题5:题面:已知向量a=(cosθ,sinθ),向量b=(,-1),则|2a-b|的最大、小值分别是()A.4,0B.4,2C.16,0D.4,0题6:题面:如图所示,在平行四边形ABCD中,,垂足为P,且,则_______.题7:题面:如图,已知,,,GB的长为,求GA,GC的长.课后练习详解题1:答案:D详解:.如图,∵a·b=0,∴a⊥b,∴∠ACB=90°,∴AB==.又CD⊥AB,∴AC2=AD·AB,∴AD=.∴AD=AB=(a-b)=a-b.所以选D题2:答案:4详解:||2=||2+||2=8,||=||,+=2,(+)·=2·=||2=4.题3:答案:A详解:,,是以为一组邻边的平行四边形的一条对角线,而是另一条对角线,表明这两条对角线互相垂直,故以为一组邻边的平行四边形为菱形.即△ABC为等腰三角形题4:答案:B详解:设D为BC的中点,可得∵∴点P满足∵向量,∴,移项得,即,得.结合D为BC的中点,可得P在BC的垂直平分线上又∵点P是△ABC的内心、外心、重心和垂心之一∴结合三角形外接圆的性质,得点P是△ABC的外心故选:B题5:答案:D详解:由于|2a-b|2=4|a|2+|b|2-4a·b=8-4(cosθ-sinθ)=8-8cos(θ+),易知0≤8-8cos(θ+)≤16,故|2a-b|的最大值和最小值分别为4和0.题6:答案:18详解:设,则,题7:答案:见详解详解:因为,所以点G为△ABC的重心,取BC的中点,连结GD,并延长GD到点E,GD=GE,连结BE,CE,所以四边形GBEC为平行四边形,,所以,在△BGE中,由正弦定理得,所以,,所以,.