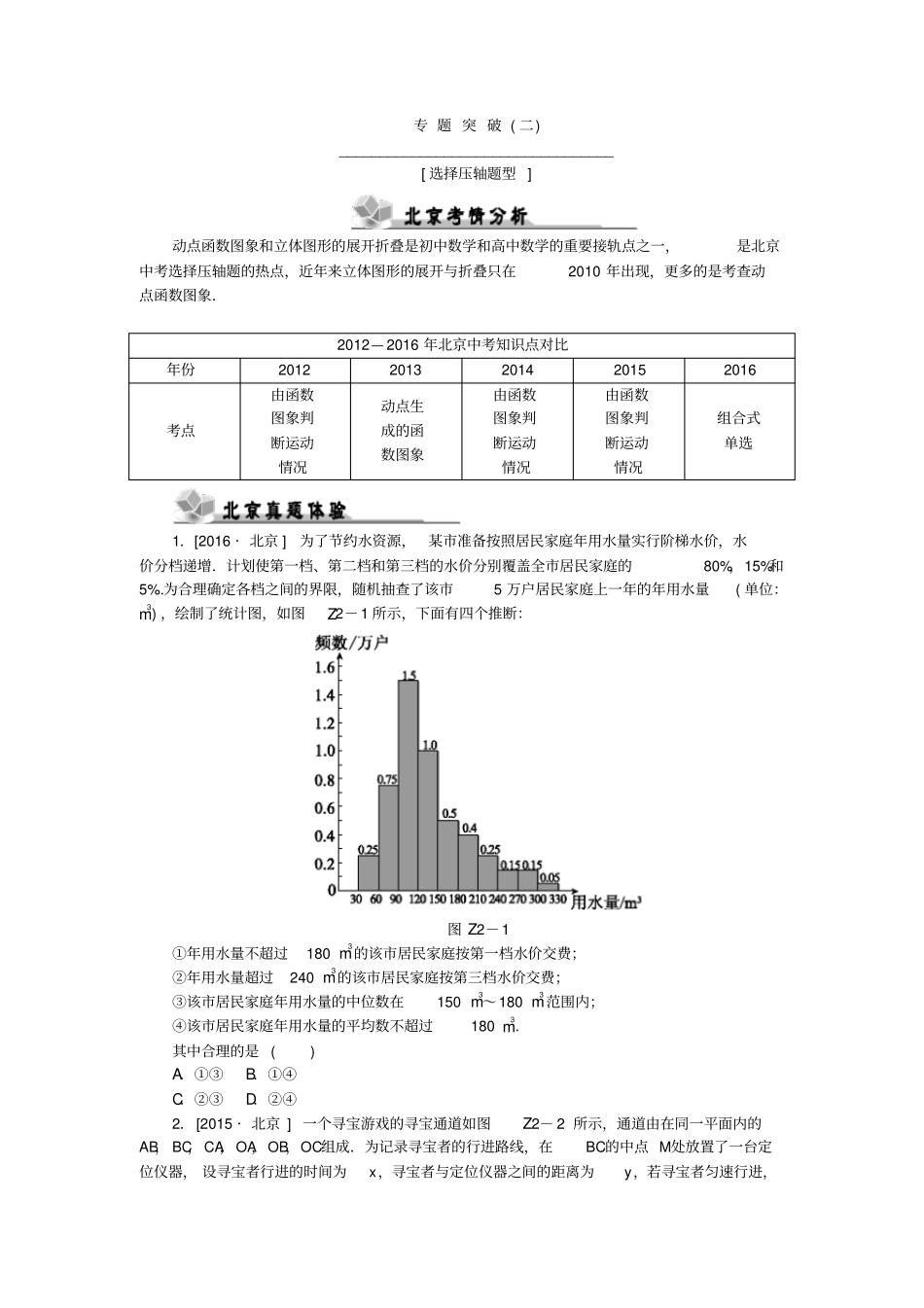
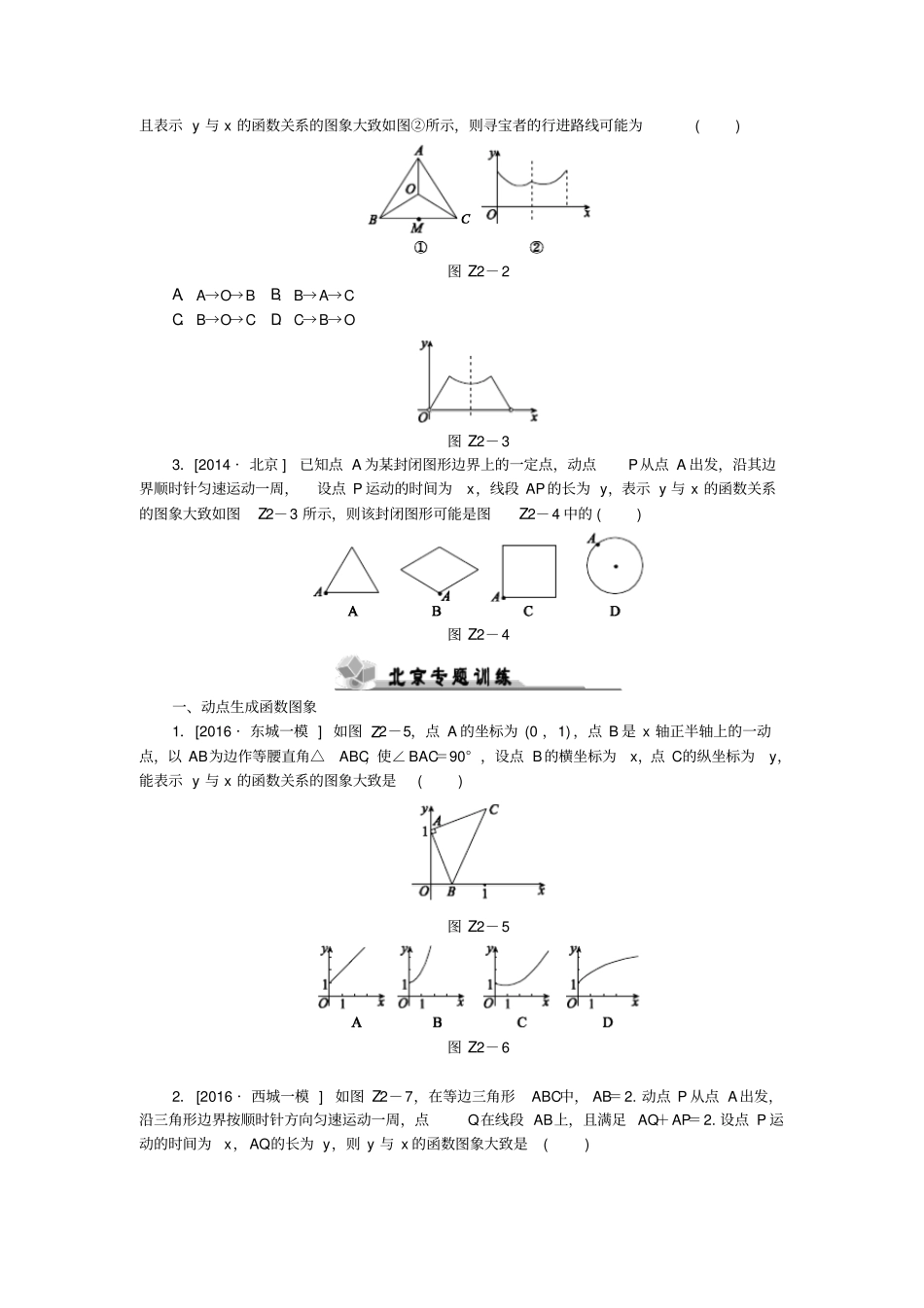
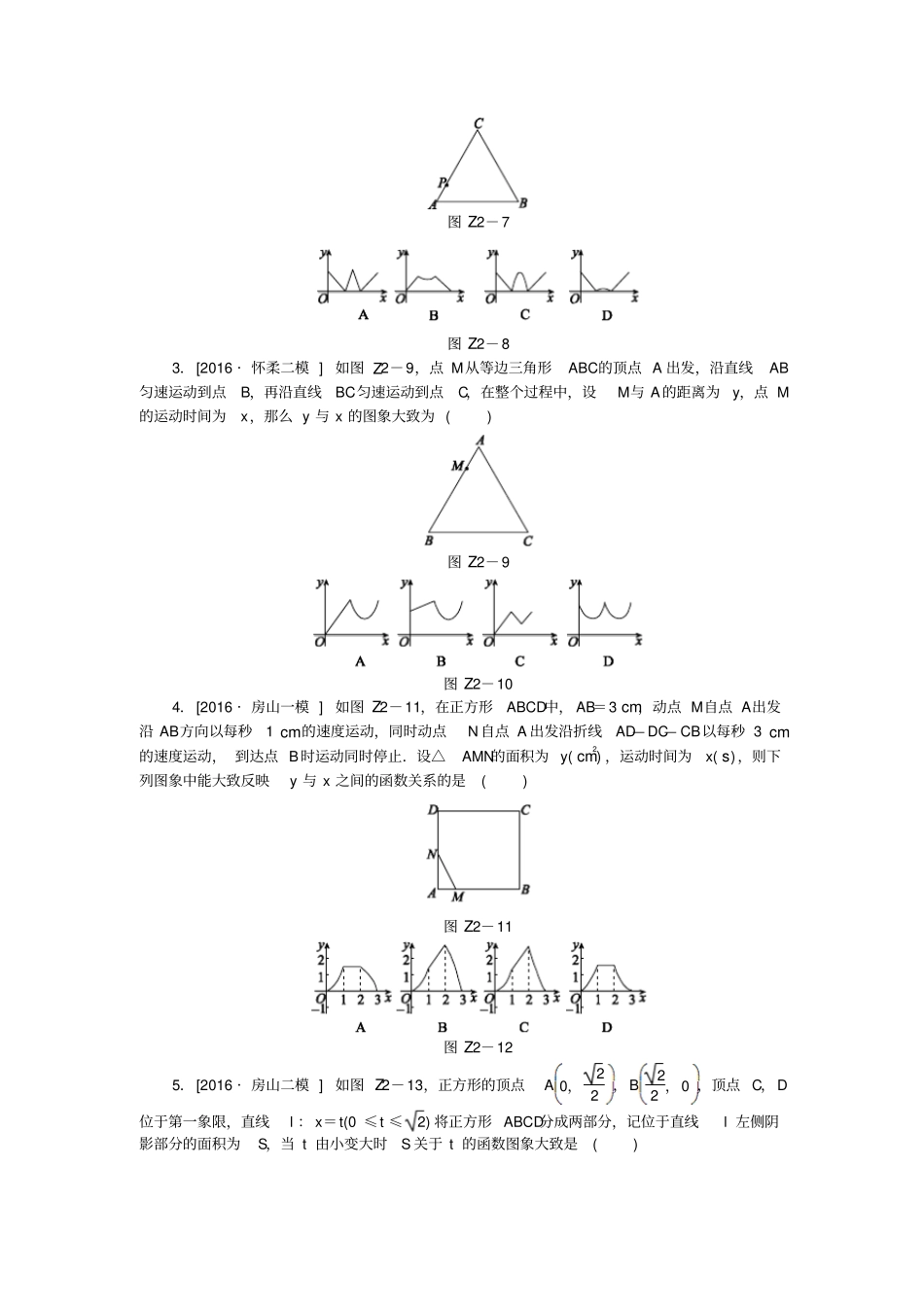
专题突破(二)__________________________________[选择压轴题型]动点函数图象和立体图形的展开折叠是初中数学和高中数学的重要接轨点之一,是北京中考选择压轴题的热点,近年来立体图形的展开与折叠只在2010年出现,更多的是考查动点函数图象.2012—2016年北京中考知识点对比年份20122013201420152016考点由函数图象判断运动情况动点生成的函数图象由函数图象判断运动情况由函数图象判断运动情况组合式单选1.[2016·北京]为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价,水价分档递增.计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%.为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图,如图Z2-1所示,下面有四个推断:图Z2-1①年用水量不超过180m3的该市居民家庭按第一档水价交费;②年用水量超过240m3的该市居民家庭按第三档水价交费;③该市居民家庭年用水量的中位数在150m3~180m3范围内;④该市居民家庭年用水量的平均数不超过180m3.其中合理的是()A.①③B.①④C.②③D.②④2.[2015·北京]一个寻宝游戏的寻宝通道如图Z2-2所示,通道由在同一平面内的AB,BC,CA,OA,OB,OC组成.为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图象大致如图②所示,则寻宝者的行进路线可能为()图Z2-2A.A→O→BB.B→A→CC.B→O→CD.C→B→O图Z2-33.[2014·北京]已知点A为某封闭图形边界上的一定点,动点P从点A出发,沿其边界顺时针匀速运动一周,设点P运动的时间为x,线段AP的长为y,表示y与x的函数关系的图象大致如图Z2-3所示,则该封闭图形可能是图Z2-4中的()图Z2-4一、动点生成函数图象1.[2016·东城一模]如图Z2-5,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是()图Z2-5图Z2-62.[2016·西城一模]如图Z2-7,在等边三角形ABC中,AB=2.动点P从点A出发,沿三角形边界按顺时针方向匀速运动一周,点Q在线段AB上,且满足AQ+AP=2.设点P运动的时间为x,AQ的长为y,则y与x的函数图象大致是()图Z2-7图Z2-83.[2016·怀柔二模]如图Z2-9,点M从等边三角形ABC的顶点A出发,沿直线AB匀速运动到点B,再沿直线BC匀速运动到点C,在整个过程中,设M与A的距离为y,点M的运动时间为x,那么y与x的图象大致为()图Z2-9图Z2-104.[2016·房山一模]如图Z2-11,在正方形ABCD中,AB=3cm,动点M自点A出发沿AB方向以每秒1cm的速度运动,同时动点N自点A出发沿折线AD—DC—CB以每秒3cm的速度运动,到达点B时运动同时停止.设△AMN的面积为y(cm2),运动时间为x(s),则下列图象中能大致反映y与x之间的函数关系的是()图Z2-11图Z2-125.[2016·房山二模]如图Z2-13,正方形的顶点A0,22,B22,0,顶点C,D位于第一象限,直线l:x=t(0≤t≤2)将正方形ABCD分成两部分,记位于直线l左侧阴影部分的面积为S,当t由小变大时S关于t的函数图象大致是()图Z2-13图Z2-146.[2016·丰台一模]如图Z2-15,矩形ABCD中,AB=2,BC=1,O是AB的中点,动点P从B点开始沿着边BC,CD运动到点D结束.设BP=x,OP=y,则y关于x的函数图象大致为()图Z2-15图Z2-167.[2016·延庆一模]如图Z2-17,大小两个正方形在同一水平线上,小正方形从图①的位置开始,匀速向右平移,到图③的位置停止运动.如果设运动时间为x,大小正方形重叠部分的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是()图Z2-17图Z2-18二、由函数图象判断运动情况图Z2-198.[2016·顺义二模]已知点M为某封闭图形边界上一定点,动点P从点M出发,沿其边界逆时针运动一周,设点P走过的路程为x,线段MP的长为y,表示y与x的函数关系的图象大致如图Z2-19所示,则该封闭图形可能是()图Z2-20图Z2-219.[2016·怀柔一模]甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(km)与甲车...