高三数学立体几何中的证明人教实验版（A）知识精讲VIP免费

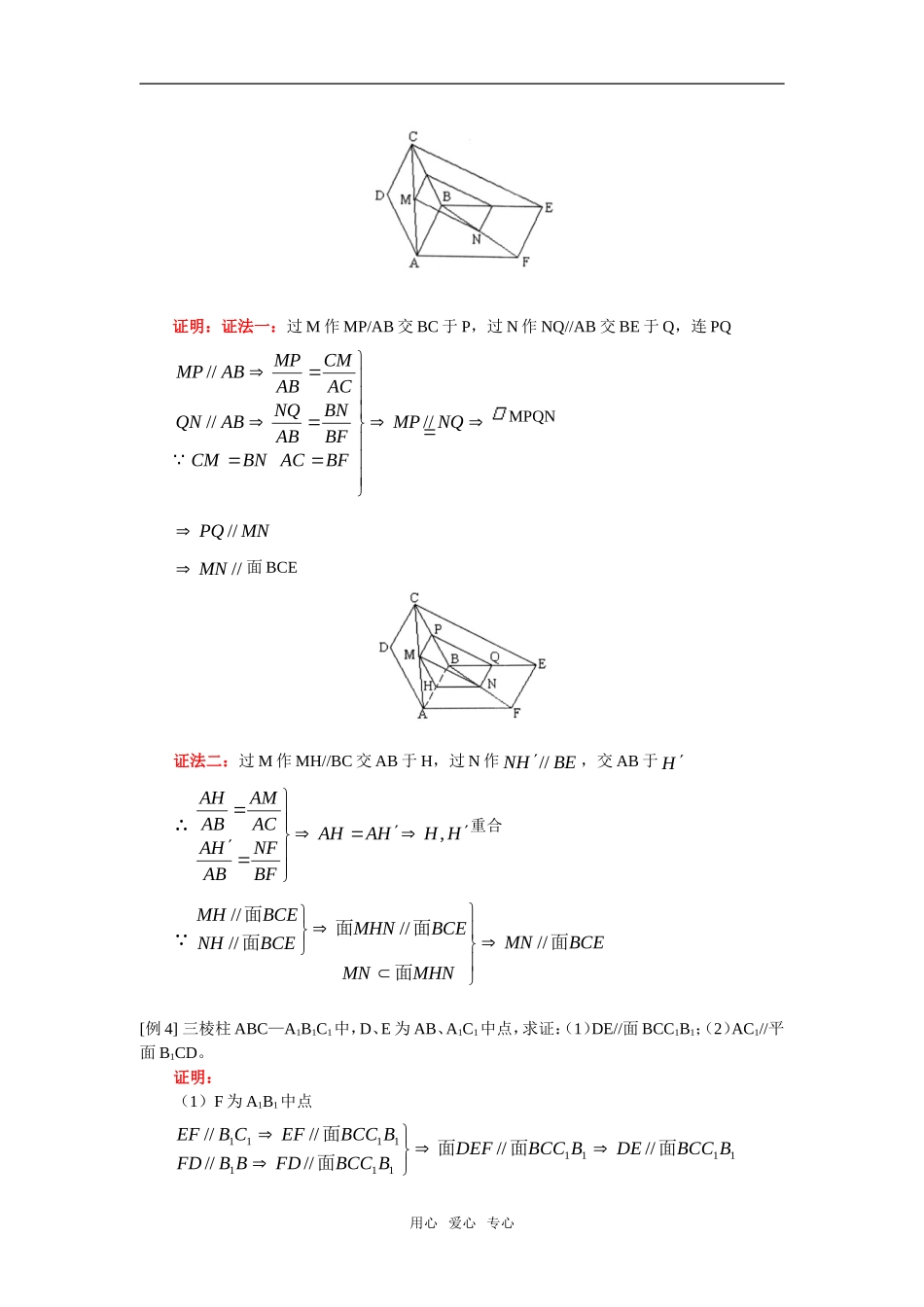
高三数学立体几何中的证明人教实验版（A）【本讲教育信息】一.教学内容：立体几何中的证明二.重点、难点：1.平面几何中的一些结论（1）中点，中位线（2）平行四边形（3）等腰三角形，中点（4）勾股定理（5）菱形，矩形2.立体几何中的定义，判定定理，性质定理3.立体几何中的精典的结论（见例1）【典型例题】[例1]以下结论中正确的作“√”，不正确的画“×”（1）①balbla//////②baba//////③//////alla④//////aa⑤//////ll⑥//////（2）①balbla//②baba//③//alla④//aa⑤//ll⑥//（3）①balbla//②baba//③alla//④aa//用心爱心专心⑤alal//⑥aa//⑦ll//⑧//答案：（1）①⑥√；②③④⑤×（2）②⑥√；①③④⑤×（3）①②④⑤⑦⑧√；③⑥×[例2]异面直线ba,，aCBA,,，bFED,,，AD，DB，BE，EC，CF中点依次为M、N、P、Q、R，求证：M、N、P、Q、R五点共面。证明：如图PQMNaPQaMN//////∴MN、PQ确定平面同理NP//QR，确定平面∴,有三个公共点，N、P、QN、P、Q不共线确定唯一一个平面∴,重合∴M、N、P、Q、R共面推广：连接异面直线ba,所有线段中点共面[例3]如图正方形ABCD，ABEF，M∈AC，N∈BF，且AM=FN，求证：MN//面BCE。用心爱心专心证明：证法一：过M作MP/AB交BC于P，过N作NQ//AB交BE于Q，连PQNQMPBFACBNCMBFBNABNQABQNACCMABMPABMP//////MPQNMNPQ////MN面BCE证法二：过M作MH//BC交AB于H，过N作BEHN//，交AB于H∴HHHAAHBFNFABHAACAMABAH,重合 BCEMNMHNMNBCEMHNBCENHBCEMH面面面面面面////////[例4]三棱柱ABC—A1B1C1中，D、E为AB、A1C1中点，求证：（1）DE//面BCC1B1；（2）AC1//平面B1CD。证明：（1）F为A1B1中点11111111111////////////BBCCDEBBCCDEFBBCCFDBBFDBBCCEFCBEF面面面面面用心爱心专心DBEHABBDBAEHCBH//21//21//1111中点为或DBHEED//BHDE//面BCC1B1（2）MCBBC11D、M中点DM//AC1AC1//面CDB1[例5]如图，正方体ABCD—A1B1C1D1中，侧面对角线AB1，BC1上分别有两点E，F，且B1E=C1F，求证：EF//平面ABCD。分析：用线面平行的判定定理来证，或用面面平行的性质定理来证。证明：证法一：分别过E，F作EM⊥AB于M，FN⊥BC于N，连结MN BB1⊥平面ABCD∴BB1⊥AB，BB1⊥BC∴EM//BB1，FN//BB1∴EM//FN又B1E=C1F∴EM=FN故四边形MNFE是∴EF//MN又MN在平面ABCD中，∴EF//平面ABCD证法二：过E作EG//AB交BB1于G，连结GF，则BBGBABEB1111用心爱心专心 B1E=C1F，B1A=C1B∴BBGBBCFC1111∴FG//B1C1//BC又EG∩FG=G，AB∩BC=B∴平面EFG//平面ABCD，而EF平面EFG∴EF//平面ABCD[例6]平面//平面，A，C，B，D，AB=a是,的公垂线，CD是斜线，若AC=BD=b，CD=c，M，N分别是AB和CD的中点。（1）求证：MN//平面；（2）求MN的长。解析：（1）证明：如图，连结AD，取AD的中点P，连结PM，PN，在△ABD中，M是AB的中点。∴PM//BD，BD平面∴PM//，同理PN//，//∴PN//，PM，PN是两相交直线∴平面PMN//平面，MN平面PMN∴MN//平面（2）连结MC，MD，在△MAC和△MBD中，AB是AC，BD的公垂线∴∠MAC=∠MBD=90°M是AB的中点，MA=MB，AC=BD∴△MAC≌△MBD，于是MC=MD，N是CD的中点∴MN⊥CD∴在△MBD中，MB=a21，BD=b∴MD=2241ab在MNDRt中，ND=c21∴222222224214141cabcabNDMDMN[例7]已知平面PAB⊥平面ABC，平面PAC⊥平面ABC，AE⊥平面PBC，E为垂足。用心爱心专心（1）求证：PA⊥平面ABC；（2）当E为△PBC的垂心时，求证：△ABC是直角三角形。证明：（1）如图，在平面ABC内取一点D，作DF⊥AC于F，平面PAC...