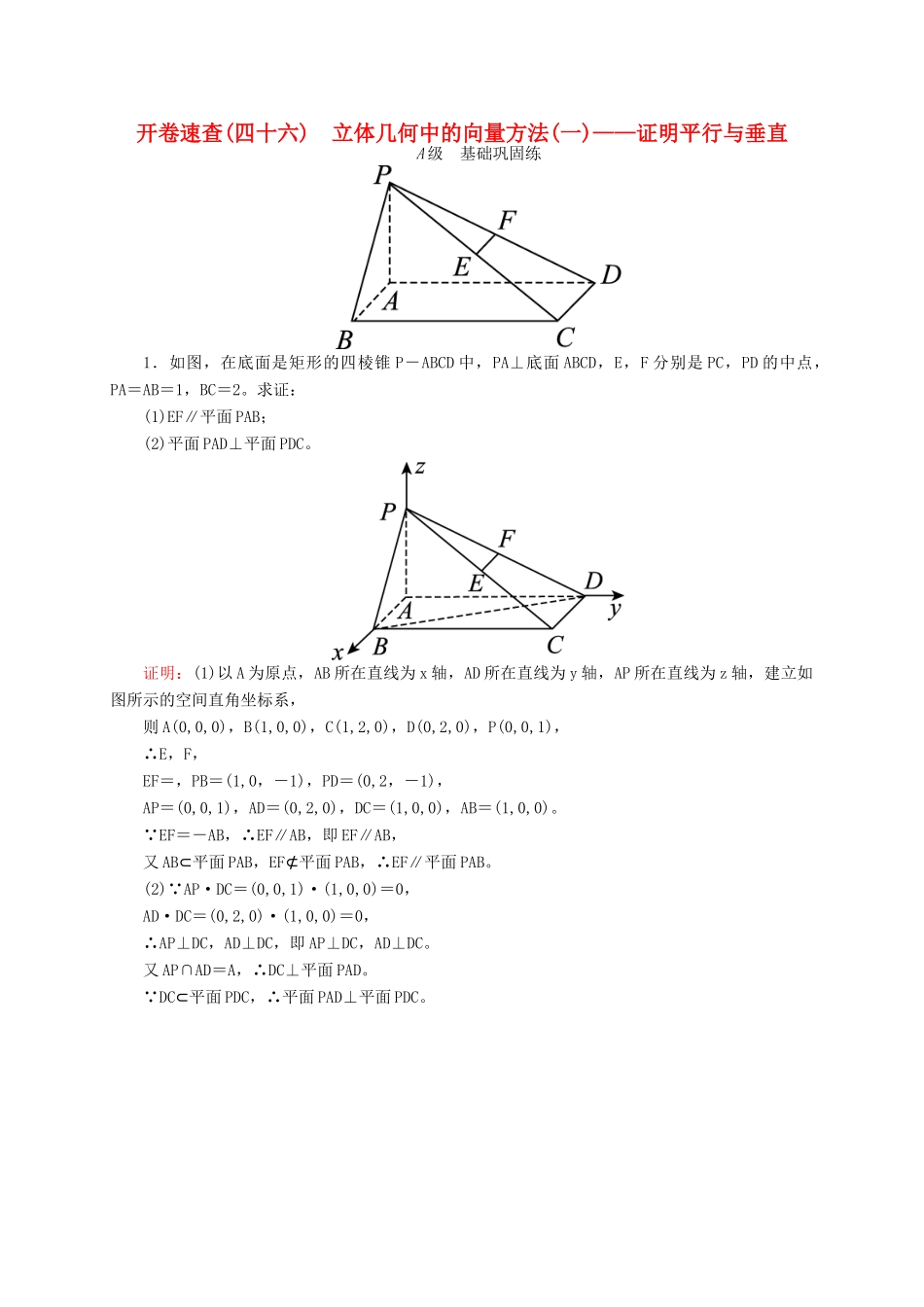
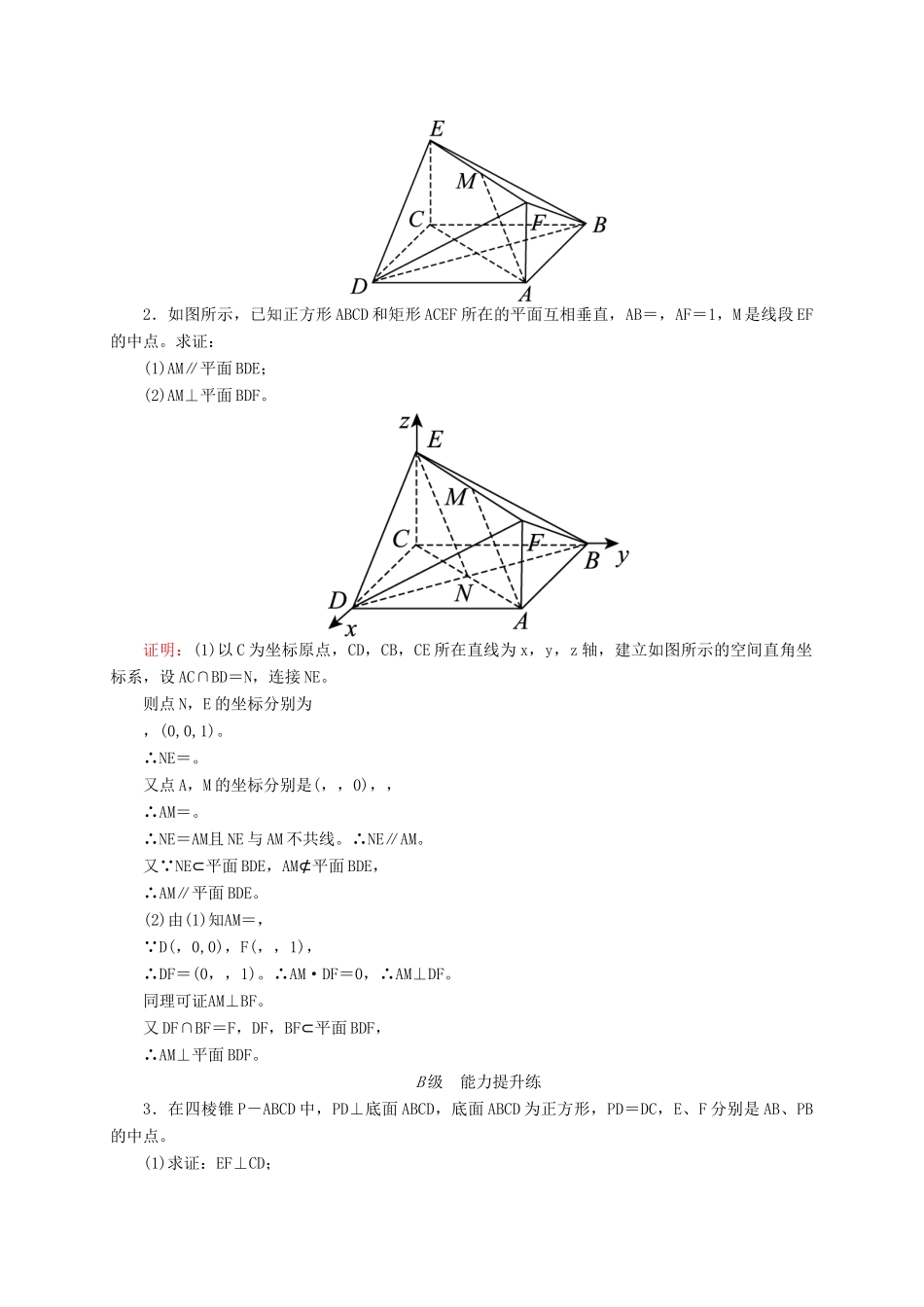
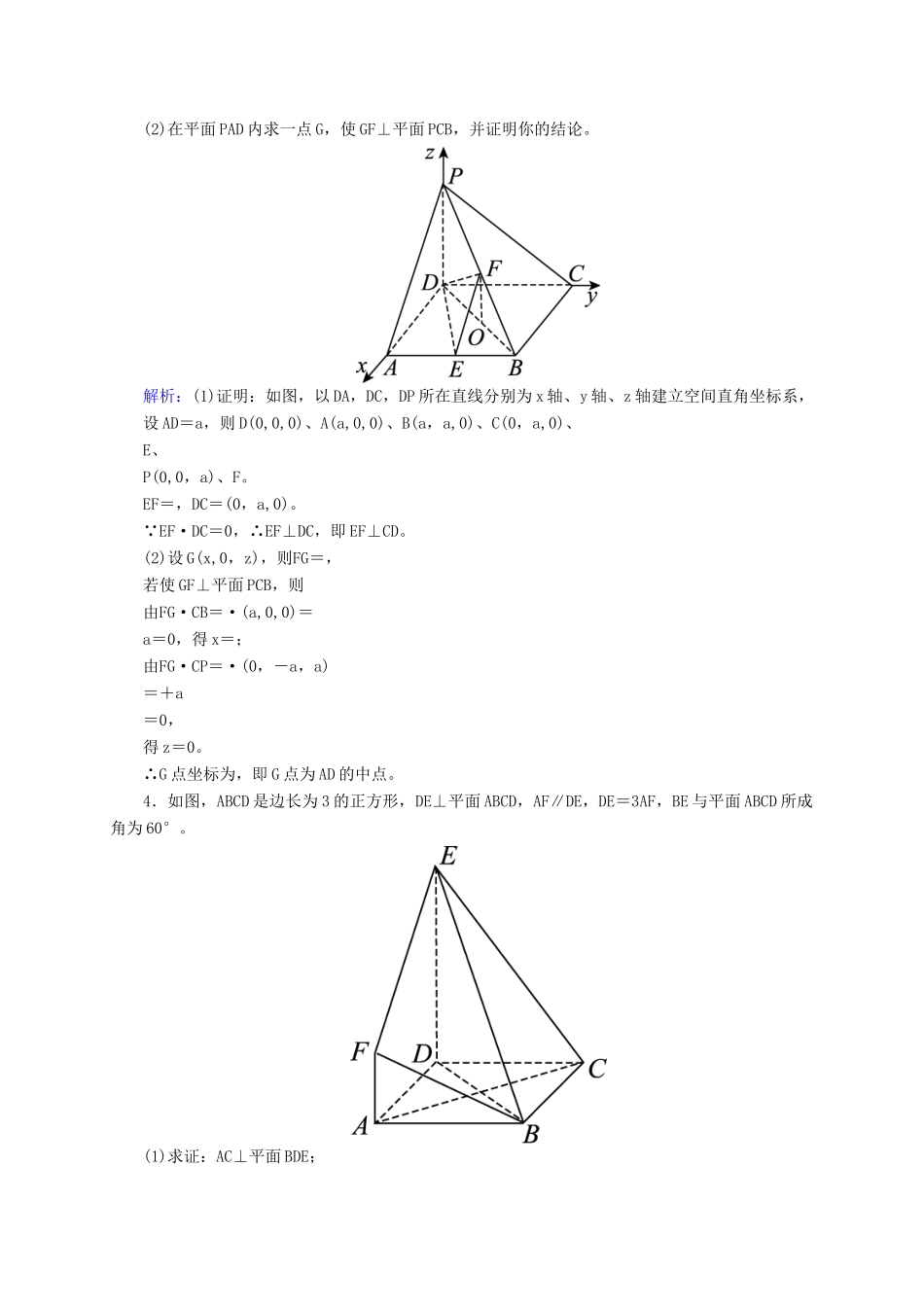
开卷速查(四十六)立体几何中的向量方法(一)——证明平行与垂直A级基础巩固练1.如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,E,F分别是PC,PD的中点,PA=AB=1,BC=2。求证:(1)EF∥平面PAB;(2)平面PAD⊥平面PDC。证明:(1)以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴,建立如图所示的空间直角坐标系,则A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),P(0,0,1),∴E,F,EF=,PB=(1,0,-1),PD=(0,2,-1),AP=(0,0,1),AD=(0,2,0),DC=(1,0,0),AB=(1,0,0)。∵EF=-AB,∴EF∥AB,即EF∥AB,又AB⊂平面PAB,EF⊄平面PAB,∴EF∥平面PAB。(2)∵AP·DC=(0,0,1)·(1,0,0)=0,AD·DC=(0,2,0)·(1,0,0)=0,∴AP⊥DC,AD⊥DC,即AP⊥DC,AD⊥DC。又AP∩AD=A,∴DC⊥平面PAD。∵DC⊂平面PDC,∴平面PAD⊥平面PDC。2.如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=,AF=1,M是线段EF的中点。求证:(1)AM∥平面BDE;(2)AM⊥平面BDF。证明:(1)以C为坐标原点,CD,CB,CE所在直线为x,y,z轴,建立如图所示的空间直角坐标系,设AC∩BD=N,连接NE。则点N,E的坐标分别为,(0,0,1)。∴NE=。又点A,M的坐标分别是(,,0),,∴AM=。∴NE=AM且NE与AM不共线。∴NE∥AM。又∵NE⊂平面BDE,AM⊄平面BDE,∴AM∥平面BDE。(2)由(1)知AM=,∵D(,0,0),F(,,1),∴DF=(0,,1)。∴AM·DF=0,∴AM⊥DF。同理可证AM⊥BF。又DF∩BF=F,DF,BF⊂平面BDF,∴AM⊥平面BDF。B级能力提升练3.在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E、F分别是AB、PB的中点。(1)求证:EF⊥CD;(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论。解析:(1)证明:如图,以DA,DC,DP所在直线分别为x轴、y轴、z轴建立空间直角坐标系,设AD=a,则D(0,0,0)、A(a,0,0)、B(a,a,0)、C(0,a,0)、E、P(0,0,a)、F。EF=,DC=(0,a,0)。∵EF·DC=0,∴EF⊥DC,即EF⊥CD。(2)设G(x,0,z),则FG=,若使GF⊥平面PCB,则由FG·CB=·(a,0,0)=a=0,得x=;由FG·CP=·(0,-a,a)=+a=0,得z=0。∴G点坐标为,即G点为AD的中点。4.如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°。(1)求证:AC⊥平面BDE;(2)设点M是线段BD上一个动点,试确定M的位置,使得AM∥平面BEF,并证明你的结论。解析:(1)证明:∵DE⊥平面ABCD,∴DE⊥AC。∵ABCD是正方形,∴AC⊥BD。从而AC⊥平面BDE。(2)∵DA,DC,DE两两垂直,∴建立空间直角坐标系D-xyz如图所示。∵BE与平面ABCD所成角为60°,即∠DBE=60°,∴=。∵正方形ABCD的边长为3,∴BD=3,∴DE=3,AF=。则A(3,0,0),F(3,0,),E(0,0,3),B(3,3,0),C(0,3,0)。∴BF=(0,-3,),EF=(3,0,-2)。设平面BEF的法向量为n=(x,y,z),则即令z=,则n=(4,2,)。点M是线段BD上一个动点,设M(t,t,0),则AM=(t-3,t,0)。∵AM∥平面BEF,∴AM·n=0。即4(t-3)+2t=0,解得t=2。此时,点M为(2,2,0),BM=BD,符合题意。