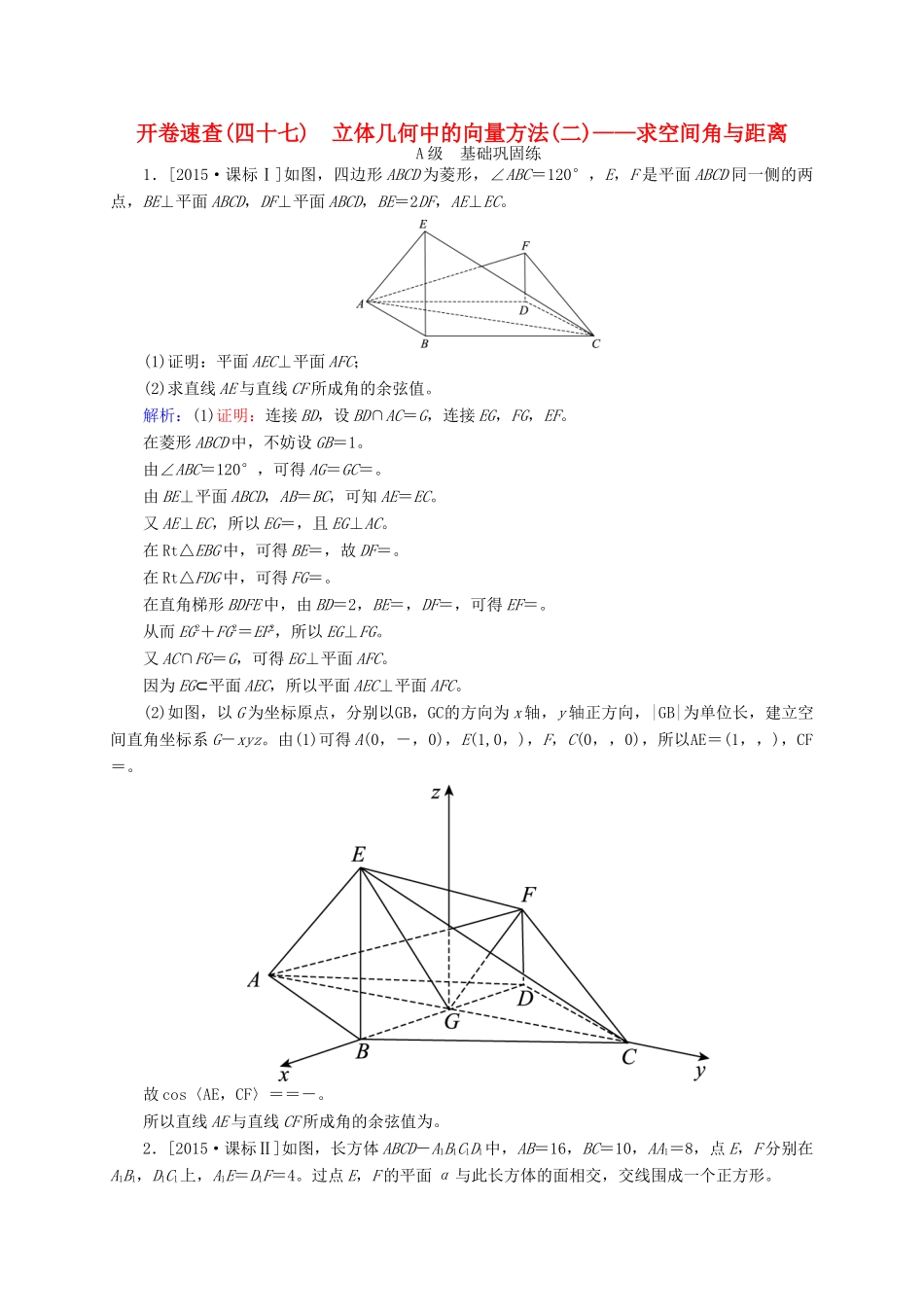
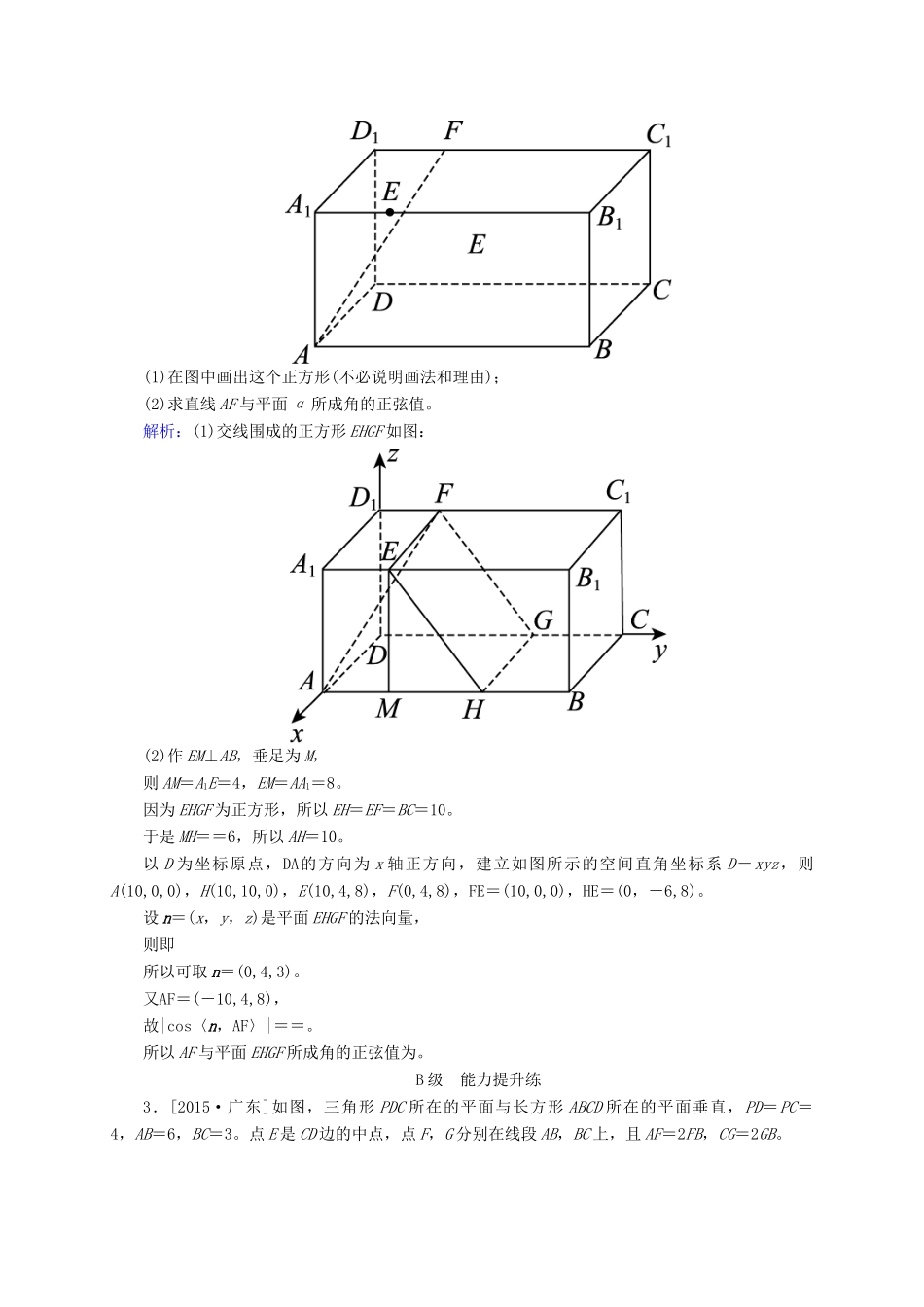
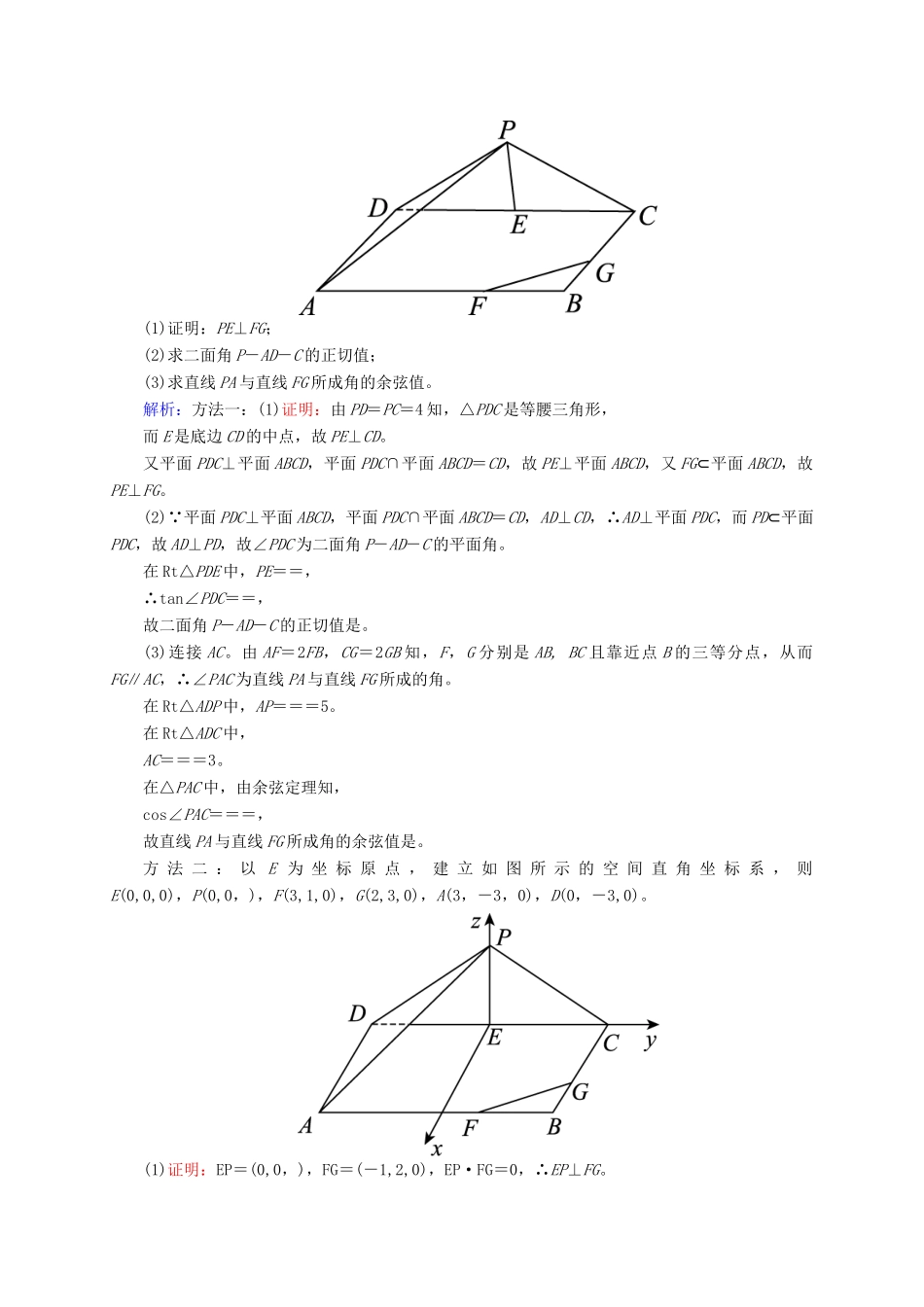
开卷速查(四十七)立体几何中的向量方法(二)——求空间角与距离A级基础巩固练1.[2015·课标Ⅰ]如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC。(1)证明:平面AEC⊥平面AFC;(2)求直线AE与直线CF所成角的余弦值。解析:(1)证明:连接BD,设BD∩AC=G,连接EG,FG,EF。在菱形ABCD中,不妨设GB=1。由∠ABC=120°,可得AG=GC=。由BE⊥平面ABCD,AB=BC,可知AE=EC。又AE⊥EC,所以EG=,且EG⊥AC。在Rt△EBG中,可得BE=,故DF=。在Rt△FDG中,可得FG=。在直角梯形BDFE中,由BD=2,BE=,DF=,可得EF=。从而EG2+FG2=EF2,所以EG⊥FG。又AC∩FG=G,可得EG⊥平面AFC。因为EG⊂平面AEC,所以平面AEC⊥平面AFC。(2)如图,以G为坐标原点,分别以GB,GC的方向为x轴,y轴正方向,|GB|为单位长,建立空间直角坐标系G-xyz。由(1)可得A(0,-,0),E(1,0,),F,C(0,,0),所以AE=(1,,),CF=。故cos〈AE,CF〉==-。所以直线AE与直线CF所成角的余弦值为。2.[2015·课标Ⅱ]如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4。过点E,F的平面α与此长方体的面相交,交线围成一个正方形。(1)在图中画出这个正方形(不必说明画法和理由);(2)求直线AF与平面α所成角的正弦值。解析:(1)交线围成的正方形EHGF如图:(2)作EM⊥AB,垂足为M,则AM=A1E=4,EM=AA1=8。因为EHGF为正方形,所以EH=EF=BC=10。于是MH==6,所以AH=10。以D为坐标原点,DA的方向为x轴正方向,建立如图所示的空间直角坐标系D-xyz,则A(10,0,0),H(10,10,0),E(10,4,8),F(0,4,8),FE=(10,0,0),HE=(0,-6,8)。设n=(x,y,z)是平面EHGF的法向量,则即所以可取n=(0,4,3)。又AF=(-10,4,8),故|cos〈n,AF〉|==。所以AF与平面EHGF所成角的正弦值为。B级能力提升练3.[2015·广东]如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3。点E是CD边的中点,点F,G分别在线段AB,BC上,且AF=2FB,CG=2GB。(1)证明:PE⊥FG;(2)求二面角P-AD-C的正切值;(3)求直线PA与直线FG所成角的余弦值。解析:方法一:(1)证明:由PD=PC=4知,△PDC是等腰三角形,而E是底边CD的中点,故PE⊥CD。又平面PDC⊥平面ABCD,平面PDC∩平面ABCD=CD,故PE⊥平面ABCD,又FG⊂平面ABCD,故PE⊥FG。(2)∵平面PDC⊥平面ABCD,平面PDC∩平面ABCD=CD,AD⊥CD,∴AD⊥平面PDC,而PD⊂平面PDC,故AD⊥PD,故∠PDC为二面角P-AD-C的平面角。在Rt△PDE中,PE==,∴tan∠PDC==,故二面角P-AD-C的正切值是。(3)连接AC。由AF=2FB,CG=2GB知,F,G分别是AB,BC且靠近点B的三等分点,从而FG∥AC,∴∠PAC为直线PA与直线FG所成的角。在Rt△ADP中,AP===5。在Rt△ADC中,AC===3。在△PAC中,由余弦定理知,cos∠PAC===,故直线PA与直线FG所成角的余弦值是。方法二:以E为坐标原点,建立如图所示的空间直角坐标系,则E(0,0,0),P(0,0,),F(3,1,0),G(2,3,0),A(3,-3,0),D(0,-3,0)。(1)证明:EP=(0,0,),FG=(-1,2,0),EP·FG=0,∴EP⊥FG。(2)平面ADC的一个法向量为n1=(0,0,1),设平面PAD的法向量为n2=(x,y,z),则取y=1,则x=0,z=-,∴n2=为平面PAD的一个法向量,∴cos〈n1,n2〉===-。记所求二面角的大小为θ,显然θ为锐角,∴cosθ=,tanθ=。(3)∵AP=(-3,3,),FG=(-1,2,0),∴cos〈AP,FG〉===,∴直线PA与直线FG所成角的余弦值为。4.[2015·陕西]如图1,在直角梯形ABCD中,AD∥BC,∠BAD=,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点。将△ABE沿BE折起到△A1BE的位置,如图2。图1图2(1)证明:CD⊥平面A1OC;(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD夹角的余弦值。解析:(1)证明:在题图1中,因为AB=BC=1,AD=2,E是AD的中点,∠BAD=,所以BE⊥AC。即在题图2中,BE⊥OA1,BE⊥OC,从而BE⊥平面A1OC,又CD∥BE,所以CD⊥平面A1OC。(2)由已知,平面A1BE⊥平面BCDE,又由(1)知,BE⊥OA1,BE⊥OC,所以∠A1OC为二面角A1-BE-C的平面角,所以∠A1OC=。如图,以O为原点,建立空间直角坐标系,因为A1B=A1E=BC=ED=1,BC∥ED,所以B,E,A1,C,得BC=,A1C=,CD=BE=(-,0,0)。设平面A1BC的法向量n1=(x1,y1,z1),平面A1CD的法向量n2=(x2,y2,z2),平面A1BC与平面A1CD夹角为θ,则得取n1=(1,1,1);得取n2=(0,1,1),从而cosθ=|cos〈n1,n2〉|==,即平面A1BC与平面A1CD夹角的余弦值为。