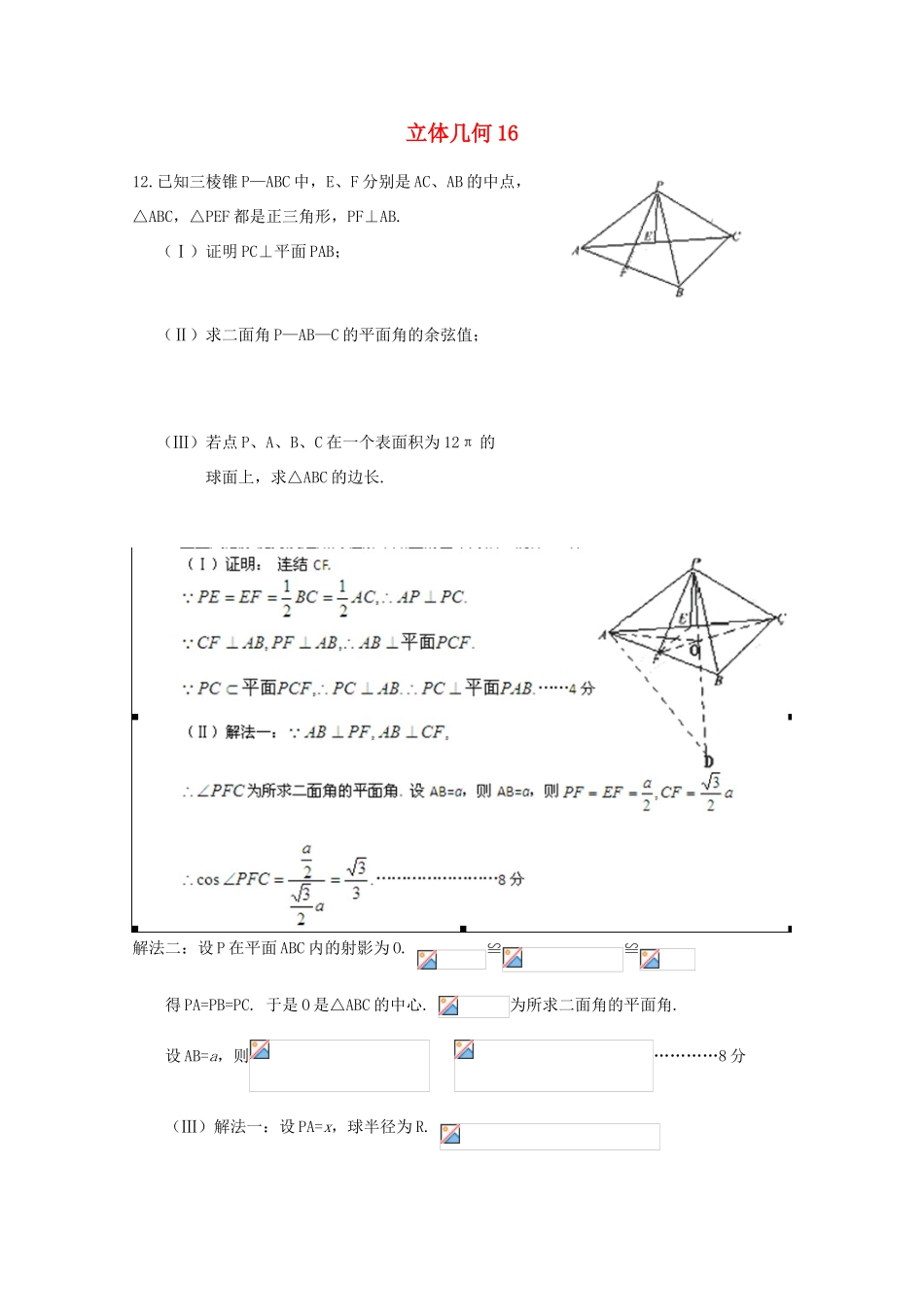
立体几何1612.已知三棱锥P—ABC中,E、F分别是AC、AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.(Ⅰ)证明PC⊥平面PAB;(Ⅱ)求二面角P—AB—C的平面角的余弦值;(Ⅲ)若点P、A、B、C在一个表面积为12π的球面上,求△ABC的边长.解法二:设P在平面ABC内的射影为O.≌≌得PA=PB=PC.于是O是△ABC的中心.为所求二面角的平面角.设AB=a,则…………8分(Ⅲ)解法一:设PA=x,球半径为R.,的边长为.………12分解法二:延长PO交球面于D,那么PD是球的直径.连结OA、AD,可知△PAD为直角三角形.设AB=x,球半径为R..……12分13.如图,在三棱柱ABC—A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,EA⊥EB1,已知AB=,BB1=2,BC=1,∠BCC1=,求:(Ⅰ)异面直线AB与EB1的距离;(Ⅱ)二面角A—EB1—A1的平面角的正切值.(Ⅱ)过E作EG//B1A1,则GE⊥面BCC1B,故GE⊥EB1且GE在圆A1B1E内,又已知AE⊥EB1故∠AEG是二面角A—EB1—A1的平面角.因EG//B1A1//BA,∠AEG=∠BAE,故解法二:(Ⅱ)由(I)可得∠AEB是二面角A—EB1—B的平面角,在Rt△ABE中,由AB=,BE=1,得tanAEB=.又由已知得平面A1B1E⊥平面BB1C1C,故二面角A—EB1—A1的平面角,故解法三:(I)以B为原点,、分别为y、z轴建立空间直角坐标系.由于BC=1,BB1=2,AB=,∠BCC1=,(II)由已知有故二面角A—EB1—A1的平面角的大小为向量的夹角.14.设函数R.(1)若处取得极值,求常数a的值;(2)若上为增函数,求a的取值范围.