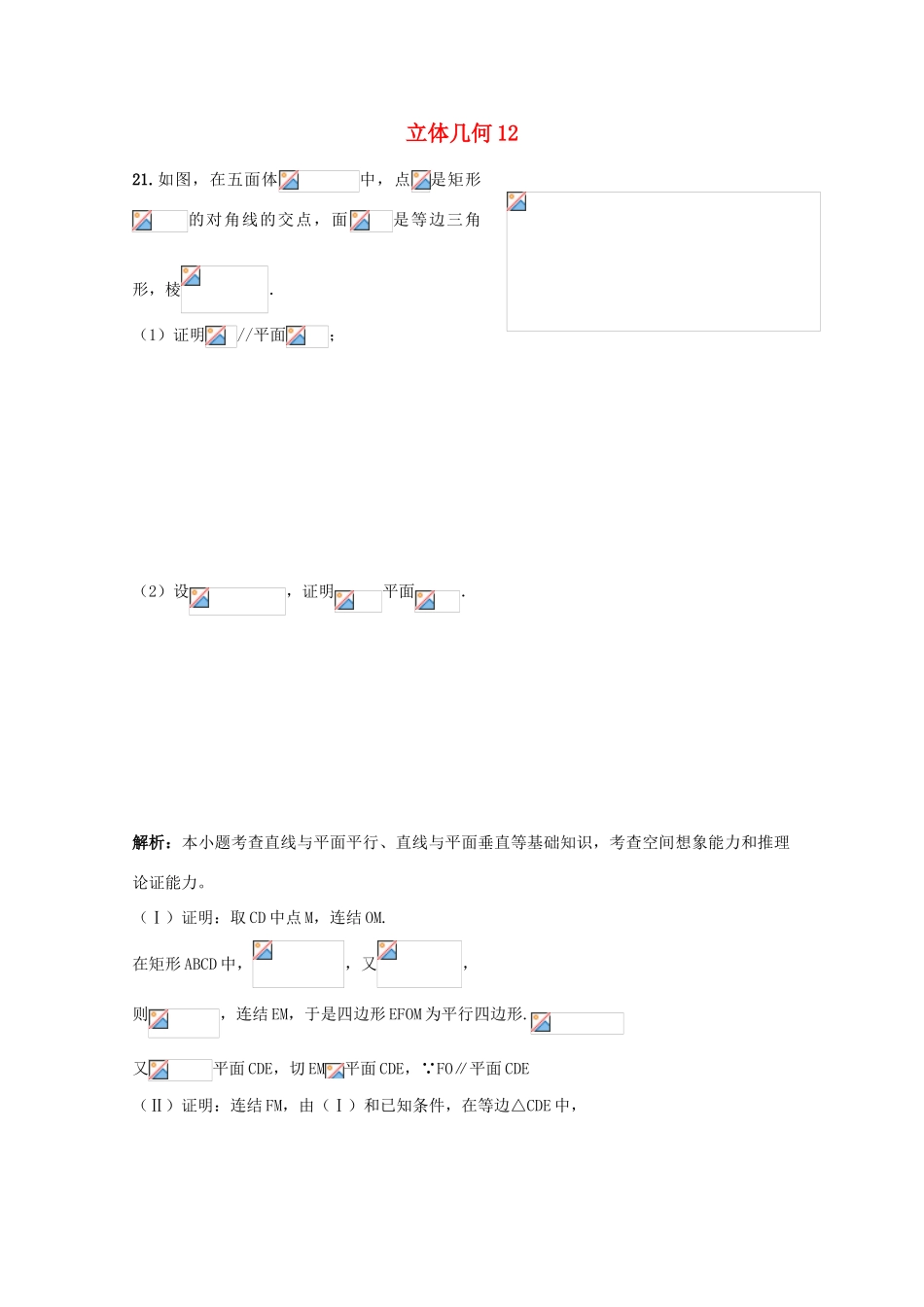
立体几何1221.如图,在五面体中,点是矩形的对角线的交点,面是等边三角形,棱.(1)证明//平面;(2)设,证明平面.解析:本小题考查直线与平面平行、直线与平面垂直等基础知识,考查空间想象能力和推理论证能力。(Ⅰ)证明:取CD中点M,连结OM.在矩形ABCD中,,又,则,连结EM,于是四边形EFOM为平行四边形.又平面CDE,切EM平面CDE,∵FO∥平面CDE(Ⅱ)证明:连结FM,由(Ⅰ)和已知条件,在等边△CDE中,且.因此平行四边形EFOM为菱形,从而EO⊥FM而FM∩CD=M,∴CD⊥平面EOM,从而CD⊥EO.而,所以EO⊥平面CDF.22.如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.(Ⅰ)求证:PB⊥DM;(Ⅱ)求CD与平面ADMN所成的角点评:本题主要考查空间线线、线面关系、空间向量的概念与运算等基础知识,同时考查空间想象能力。方法二:如图,以为坐标原点建立空间直角坐标系,设,则.(I)因为,所以(II)因为,所以,又因为,所以平面因此的余角即是与平面所成的角.因为,所以与平面所成的角为.23.如图,在四棱锥P—ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点。(Ⅰ)求证:PB⊥DM;(Ⅱ)求BD与平面ADMN所成的角。本题主要考查空间线线、线面关系、空间向量的概念与运算等基础知识,同时考查空间想象能力。满分14分。方法二:如图,以A为坐标原点建立空间直角坐标系,设BC=1,则(Ⅰ)因为,所以PB⊥DM.(Ⅱ)因为,所以PB⊥AD.又PB⊥DM.因此的余角即是BD与平面ADMN所成的角.因为,所以=,因此BD与平面ADMN所成的角为.24.如图,在四棱锥P-ABCD中,PA底面ABCD,DAB为直角,AB‖CD,AD=CD=24,E、F分别为PC、CD的中点.(Ⅰ)试证:CD平面BEF;(Ⅱ)设PA=k·AB,且二面角E-BD-C的平面角大于,求k的取值范围.解析:(I)证:由已知且为直角。故ABFD是矩形。从而。又底面ABCD,,故由三垂线定理知D中,E、F分别为PC、CD的中点,故EF//PD,从而,由此得面BEF。(II)连接AC交BF于G,易知G为AC的中点,连接EG,则在中易知EG//PA。又因PA底面ABCD,故EG底面ABCD。在底面ABCD中,过G作GHBD。垂足为H,连接EH,由三垂线定理知EHBD。从而为二面角E-BD-C的平面角。设以下计算GH,考虑底面的平面图。连结GD,因故GH=.在。而。因此,。由知是锐角。故要使,必须,解之得,中的取值范围为25.在长方体中,已知,求异面直线与所成角的大小(结果用反三角函数值表示).(坐标法)以D为坐标原点,分别以DA、DC、DD1所在直线为x轴、y轴、z轴,建立空间直角坐标系.则A1(4,0,3)、B(4,4,0)、B1(4,4,3)、C(0,4,0),得.设与的夹角为θ,则,所以与的夹角大小为,即异面直线A1B与B1C所成角的大小为.