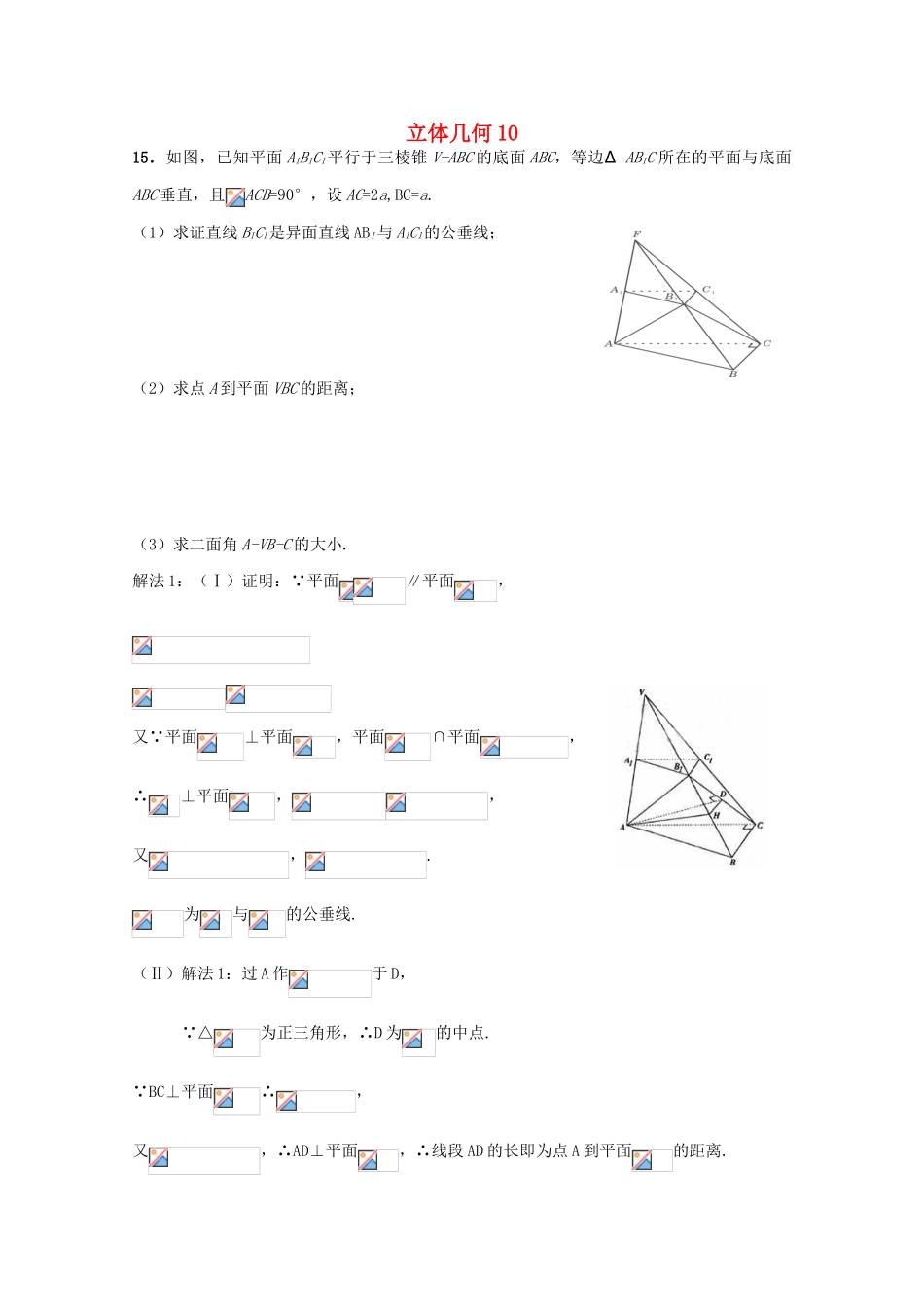
立体几何1015.如图,已知平面A1B1C1平行于三棱锥V-ABC的底面ABC,等边∆AB1C所在的平面与底面ABC垂直,且ACB=90°,设AC=2a,BC=a.(1)求证直线B1C1是异面直线AB1与A1C1的公垂线;(2)求点A到平面VBC的距离;(3)求二面角A-VB-C的大小.解法1:(Ⅰ)证明:∵平面∥平面,又∵平面⊥平面,平面∩平面,∴⊥平面,,又,.为与的公垂线.(Ⅱ)解法1:过A作于D,∵△为正三角形,∴D为的中点.∵BC⊥平面∴,又,∴AD⊥平面,∴线段AD的长即为点A到平面的距离.在正△中,.∴点A到平面的距离为.(III)过点作于,连,由三重线定理知是二面角的平面角。在中,。。所以,二面角的大小为arctan.16.如图,α⊥β,α∩β=l,A∈α,B∈β,点A在直线l上的射影为A1,点B在l的射影为B1,已知AB=2,AA1=1,BB1=,求:(Ⅰ)直线AB分别与平面α,β所成角的大小;(Ⅱ)二面角A1-AB-B1的大小.解法一:(Ⅰ)如图,连接A1B,AB1,∵α⊥β,α∩β=l,AA1⊥l,BB1⊥l,∴AA1⊥β,BB1⊥α.则∠BAB1,∠ABA1分别是AB与α和β所成的角.Rt△BB1A中,BB1=,AB=2,∴sin∠BAB1==.∴∠BAB1=45°.Rt△AA1B中,AA1=1,AB=2,sin∠ABA1==,∴∠ABA1=30°.故AB与平面α,β所成的角分别是45°,30°.(Ⅱ)∵BB1⊥α,∴平面ABB1⊥α.在平面α内过A1作A1E⊥AB1交AB1于E,则A1E⊥平面AB1B.过E作EF⊥AB交AB于F,连接A1F,则由三垂线定理得A1F⊥AB,∴∠A1FE就是所求二面角的平面角.在Rt△ABB1中,∠BAB1=45°,∴AB1=B1B=.∴Rt△AA1B中,A1B===.由AA1·A1B=A1F·AB得A1F===,∴在Rt△A1EF中,sin∠A1FE==,∴二面角A1-AB-B1的大小为arcsin.解法二:(Ⅰ)同解法一.(Ⅱ)如图,建立坐标系,则A1(0,0,0),A(0,0,1),B1(0,1,0),B(,1,0).在AB上取一点F(x,y,z),则存在t∈R,使得AF=tAB,即(x,y,z-1)=t(,1,-1),∴点F的坐标为(t,t,1-t).要使A1F⊥AB,须A1F·AB=0,即(t,t,1-t)·(,1,-1)=0,2t+t-(1-t)=0,解得t=,∴点F的坐标为(,-,),∴A1F=(,,).设E为AB1的中点,则点E的坐标为(0,,).∴EF=(,-,).又EF·AB=(,-,)·(,1,-1)=--=0,∴EF⊥AB,∴∠A1FE为所求二面角的平面角.又cos∠A1FE=====,∴二面角A1-AB-B1的大小为arccos.17.在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60.(1)求四棱锥P-ABCD的体积;(2)若E是PB的中点,求异面直线DE与PA所成角的大小(结果用反三角函数值表示).设的夹角为θ,有cosθ=,θ=arccos,∴异面直线DE与PA所成角的大小是arccos;解法二:取AB的中点F,连接EF、DF.由E是PB的中点,得EF∥PA,∴∠FED是异面直线DE与PA所成角(或它的补角),在Rt△AOB中AO=ABcos30°==OP,于是,在等腰Rt△POA中,PA=,则EF=.在正△ABD和正△PBD中,DE=DF=,cos∠FED==∴异面直线DE与PA所成角的大小是arccos.18..在直三棱柱中,.(1)求异面直线与所成的角的大小;(2)若与平面S所成角为,求三棱锥的体积。解:(1)∵BC∥B1C1,∴∠ACB为异面直线B1C1与AC所成角(或它的补角)∵∠ABC=90°,AB=BC=1,∴∠ACB=45°,∴异面直线B1C1与AC所成角为45°.(2)∵AA1⊥平面ABC,∠ACA1是A1C与平面ABC所成的角,∠ACA=45°.∵∠ABC=90°,AB=BC=1,AC=,∴AA1=.∴三棱锥A1-ABC的体积V=S△ABC×AA1=.