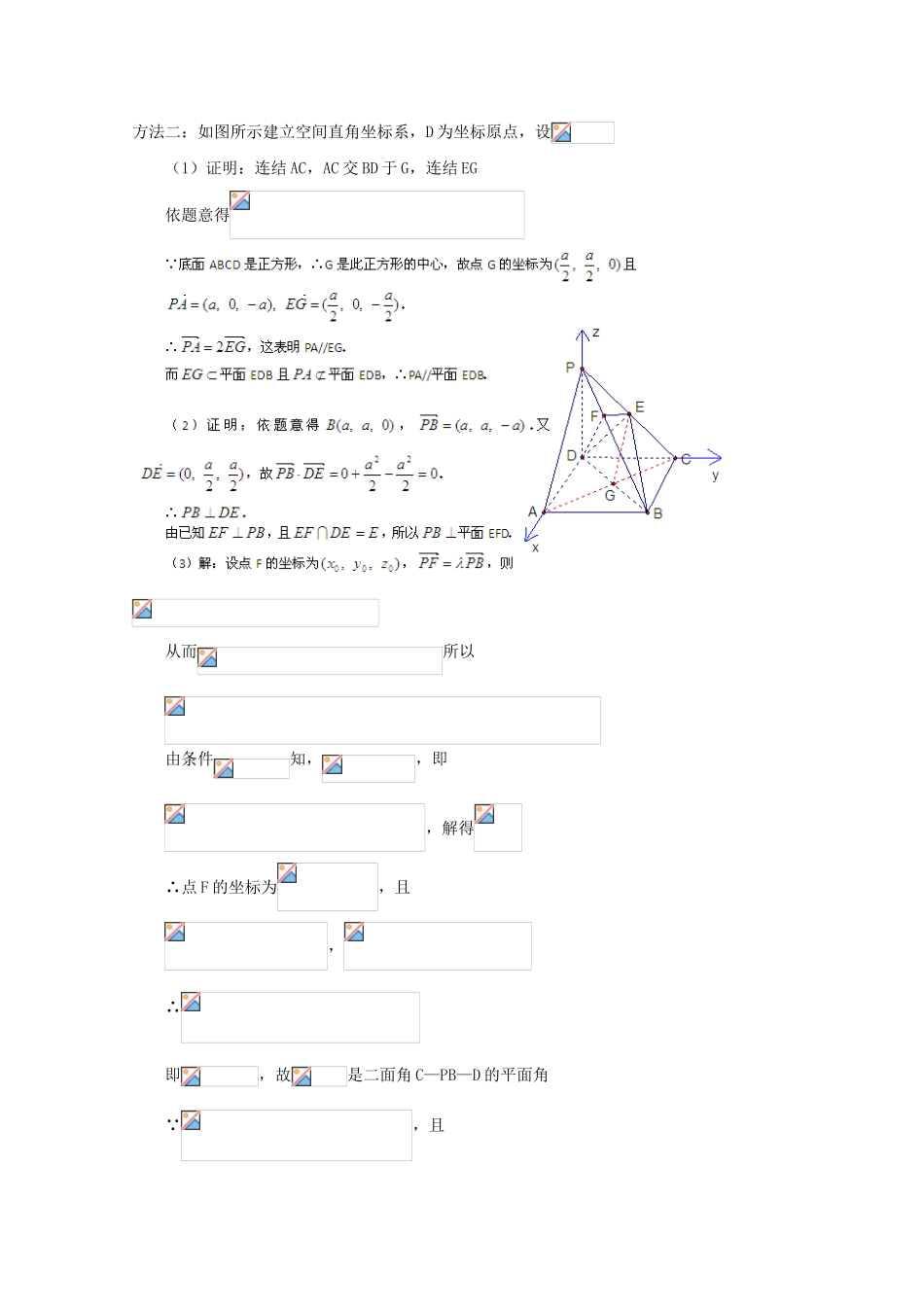
立体几何036.如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F(1)证明PA//平面EDB;(2)证明PB⊥平面EFD;(3)求二面角C—PB—D的大小解析:方法一:(1)证明:连结AC,AC交BD于O,连结EO∵底面ABCD是正方形,∴点O是AC的中点在中,EO是中位线,∴PA//EO而平面EDB且平面EDB,所以,PA//平面EDB(2)证明:∵PD⊥底面ABCD且底面ABCD,∴∵PD=DC,可知是等腰直角三角形,而DE是斜边PC的中线,∴①同样由PD⊥底面ABCD,得PD⊥BC∵底面ABCD是正方形,有DC⊥BC,∴BC⊥平面PDC而平面PDC,∴②由①和②推得平面PBC而平面PBC,∴又且,所以PB⊥平面EFD方法二:如图所示建立空间直角坐标系,D为坐标原点,设(1)证明:连结AC,AC交BD于G,连结EG依题意得从而所以由条件知,,即,解得∴点F的坐标为,且,∴即,故是二面角C—PB—D的平面角∵,且,,∴∴所以,二面角C—PB—D的大小为7.解析:方法一解:(Ⅰ)记AC与BD的交点为O,连接OE,∵O、M分别是AC、EF的中点,ACEF是矩形,∴四边形AOEM是平行四边形,∴AM∥OE∵平面BDE,平面BDE,∴AM∥平面BDE(Ⅱ)在平面AFD中过A作AS⊥DF于S,连结BS,∵AB⊥AF,AB⊥AD,∴AB⊥平面ADF,∴AS是BS在平面ADF上的射影,由三垂线定理得BS⊥DF∴∠BSA是二面角A—DF—B的平面角在RtΔASB中,∴∴二面角A—DF—B的大小为60º方法二(Ⅰ)建立如图所示的空间直角坐标系设,连接NE,则点N、E的坐标分别是(、(0,0,1),∴=(,又点A、M的坐标分别是()、(∴=(∴=且NE与AM不共线,∴NE∥AM又∵平面BDE,平面BDE,∴AM∥平面BDF(Ⅱ)∵AF⊥AB,AB⊥AD,AF∴AB⊥平面ADF∴为平面DAF的法向量∵=(·=0,∴=(·=0得,∴NE为平面BDF的法向量