高中数学研究性课题：向量在物理中的应用旧人教高中必修第一册(下)VIP免费

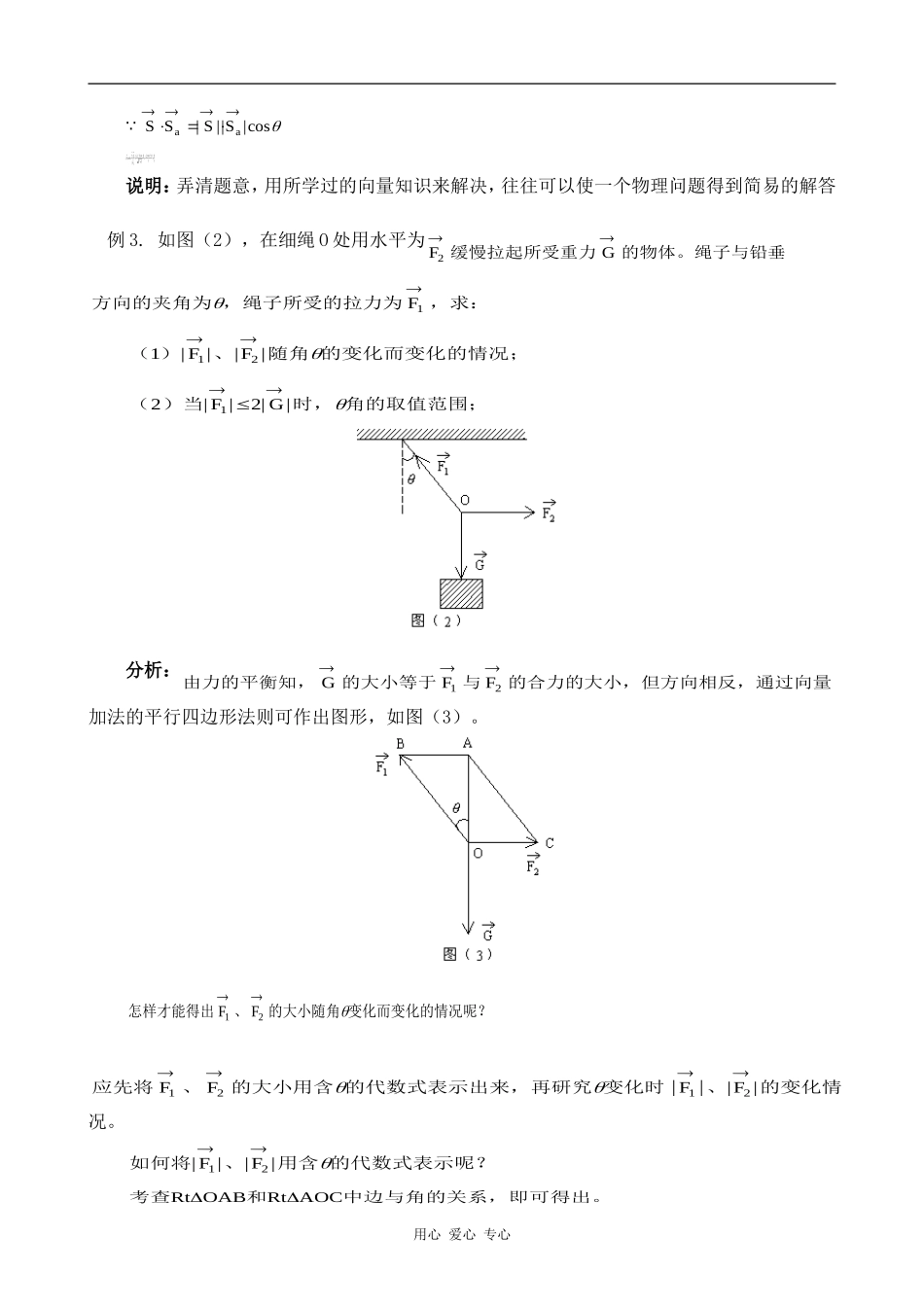
研究性课题：向量在物理中的应用一.目标：使学生会用向量的知识研究物理中的问题，把物理问题转化为数学问题，建立数学模型，研究物理现象，逐步培养学生发现问题，提出问题和明确探究方向的能力，让学生体验数学活动的过程，培养学生的创新精神和应用能力。二.重点、难点：将物理问题转化成数学问题，利用向量的知识及有关数学方法来解决问题，并解释有关的物理现象。［学法指导］向量是既有大小又有方向的量，物理中的很多量都是向量，如力、速度、加速度、位移等。力、速度、加速度、位移的合成与分解就是向量的加法、减法。动量是实数与向量的积。mv功是力与所产生的位移的数量积。Fs用向量解决物理问题的方法：把物理问题转化为数学问题，抽象成数学模型，对这个数学模型进行探究，进而解释相关物理现象。【例题分析】例1.一条河的两岸平行，河宽为dm，一船从A出发航行到河的对岸，船航行速度大小为，水流速度大小为，且，那么与的夹角多大时，船才能垂直到||||||||vvvvvv121212达河岸B处？船航行多少时间？分析：如果水是静止的，则船只要取垂直于河岸的方向行驶就行了。但由于水流动的作用船要被水冲向下游，因此要使船垂直到达对岸，就要使vv12与的合速度的方向正好垂直于河岸方向。根据题意作出图形，如图（1）。由中三边关系易求出、的合速度（即船的实际速度）的大小。RtABCvv12怎样求船航行的时间？用河的宽度除以合速度的大小即得。怎样求此时与的夹角呢？vv12用心爱心专心RtABCCCvv中，，且，由此可得出的值，的大小也就确定1801sin||||sin了。解：如图（1）设是与的合速度，由题意知vvvvvv121222||||||船航行的时间Tdvdvv||||||1222又sin()||||1801vvsin||||||(||||)vvvvv122212121又90180arcsin(||||)1212vv说明：解决此类问题的关键在于“水流速度＋航行速度＝船的实际速度”，注意“速度”是一个向量，既有大小又有方向。具体计算时要用到解三角形等知识。例2.两个粒子a、b从同一源发射出来。在某一时刻，它们的位移分别为SSab()()43210，，，。（）写出此时粒子相对粒子的位移；1baS（）计算在方向上的投影。2SSa分析：“位移”也是一个向量。粒子b相对于粒子a的位移是什么呢？粒子b相对于粒子a的位移即粒子b与粒子a位移的差向量。SSa在方向上的投影又是什么？怎样计算呢？SSSSSaa在方向上的投影是，其中为与的夹角。||cos利用向量的数量积可知，从而可求出在方向上的投影。||cos||SSSSSSaaa解：（），，，12104327SSSba()()()（）设为与的夹角，则与方向上的投影为2SSSSSaa||cos用心爱心专心SSSSaa||||cos||cos||()()SSSSaa2743432473513522，，说明：弄清题意，用所学过的向量知识来解决，往往可以使一个物理问题得到简易的解答例3.如图（2），在细绳O处用水平为FG2缓慢拉起所受重力的物体。绳子与铅垂方向的夹角为，绳子所受的拉力为，求：F1（）、随角的变化而变化的情况；112||||FF（）当时，角的取值范围；221||||FG分析：由力的平衡知，的大小等于与的合力的大小，但方向相反，通过向量GFF12加法的平行四边形法则可作出图形，如图（3）。怎样才能得出、的大小随角变化而变化的情况呢？FF12应先将、的大小用含的代数式表示出来，再研究变化时、的变化情FFFF1212||况。如何将、用含的代数式表示呢？||||FF12考查和中边与角的关系，即可得出。RtOABRtAOC用心爱心专心当时，角的取值范围又如何确定呢？||||FG12由第（）问可知，可用含的代数式表示，那么就可构造出一个含有的不等式，11||F这个不等式的解集，即为角的取值范围。解：（1）如图（3）由力的平衡及向量加法的平行四边形法则知：GFF()12解直角三角形得：||||cos||||tanFGFG12...