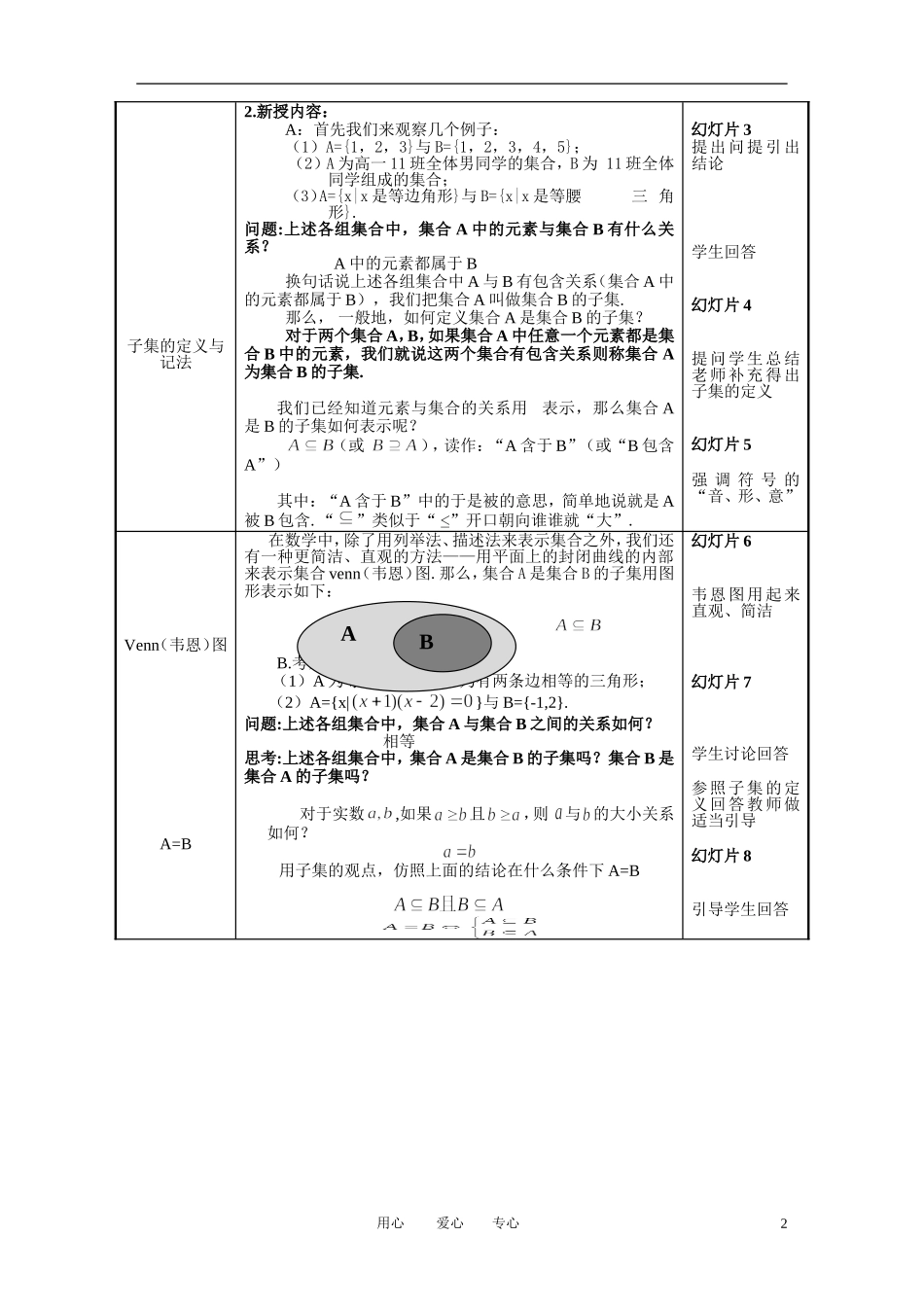
用心爱心专心1.1.2集合间的基本关系班级授课人课时第一课时课型教学目标知识技能1.了解集合之间的包含、相等关系的含义;理解子集、真子集的概念;2.能利用Venn图表达集合间的关系;了解与空集的含义.过程方法让学生通过观察具体的实例运用类比的思想,发现集合间的基本关系,体验其现实意义.情感态度价值观1.树立数形结合的思想.2.体会类比对发现新结论的作用.教学重点子集与空集的概念;用Venn图表达集合间的关系.教学难点弄清元素与子集、属于与包含之间的区别;教学方法和手段多媒体教学过程教学内容小注复习回顾1.复习引入:在前面的课程中我们学习了集合的含义与表示,我们来回顾一下:问题:(1)集合间有哪两种表示方法?列举法、描述法(2)元素与集合间有那几种关系?属于,不属于在前面的课上我曾说过实数之间有一些关系,是哪些关系呢?比如:55,57,53也就是说实数间有大小相等的关系。我们已经知道了元素与集合之间的关系,那么仿照实数之间的关系,集合与集合之间是否有类似的关系呢?(请同学们相互讨论一下)。那么今天我们就来研究集合间的基本关系,看一看是否与你们想象中的是否是一样的,有哪些差距?复习引入时间约5分钟幻灯片2举出实例,学生回答。学生会填出大于、小于相等的关系符号1用心爱心专心子集的定义与记法2.新授内容:A:首先我们来观察几个例子:(1)A={1,2,3}与B={1,2,3,4,5};(2)A为高一11班全体男同学的集合,B为11班全体同学组成的集合;(3)A={x|x是等边角形}与B={x|x是等腰三角形}.问题:上述各组集合中,集合A中的元素与集合B有什么关系?A中的元素都属于B换句话说上述各组集合中A与B有包含关系(集合A中的元素都属于B),我们把集合A叫做集合B的子集.那么,一般地,如何定义集合A是集合B的子集?对于两个集合A,B,如果集合A中任意一个元素都是集合B中的元素,我们就说这两个集合有包含关系则称集合A为集合B的子集.我们已经知道元素与集合的关系用表示,那么集合A是B的子集如何表示呢?(或),读作:“A含于B”(或“B包含A”)其中:“A含于B”中的于是被的意思,简单地说就是A被B包含.“”类似于“”开口朝向谁谁就“大”.幻灯片3提出问提引出结论学生回答幻灯片4提问学生总结老师补充得出子集的定义幻灯片5强调符号的“音、形、意”Venn(韦恩)图A=B在数学中,除了用列举法、描述法来表示集合之外,我们还有一种更简洁、直观的方法——用平面上的封闭曲线的内部来表示集合venn(韦恩)图.那么,集合A是集合B的子集用图形表示如下:B.考察下列各组集合:(1)A为等腰三角形与B为有两条边相等的三角形;(2)A={x|}与B={-1,2}.问题:上述各组集合中,集合A与集合B之间的关系如何?相等思考:上述各组集合中,集合A是集合B的子集吗?集合B是集合A的子集吗?对于实数,如果且,则与的大小关系如何?用子集的观点,仿照上面的结论在什么条件下A=B幻灯片6韦恩图用起来直观、简洁幻灯片7学生讨论回答参照子集的定义回答教师做适当引导幻灯片8引导学生回答2AB用心爱心专心真子集的定义与记法若,则集合A与B一定相等吗?若,则可能有A=B,也可能.当,且时,我们如何进行数学解释?如果,但存在元素且,则称集合A是集合B的真子集.AB(或BA)举例(由学生举例,共同辨析)A=BAB幻灯片9需要学生注意空集的记法和定义C:(1)(2)上述两个集合有何共同特点?集合中没有元素我们就把上述集合称为空集不含任何元素的集合叫做空集,记为规定:空集是任何集合的子集空集与集合{0}相等吗?{0}空集是任何非空集合的真子集幻灯片10引出空集幻灯片11结论通过前面的学习我们可以知道:1)任何集合是它本身的子集2)对于集合A,B,C,如果,且,那么幻灯片12用韦恩图在ppt中动态展示出来例题例题:写出集合{a,b,c}的所有子集并指出,真子集、非空真子集.解:集合{a,b,c}子集:,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}集合{a,b,c}真子集,{a},{b},{c},{a,b},{a,c},{b,c}集合{a,b,c}的非空真子集{a},{b},{c},{a,b},{a,c},{b,c}幻灯片13理解提高注意空集与全集写子集时不要少写,元素的个数由少到多3本课小结本节课我们学习了集合间的基本关系,本节...