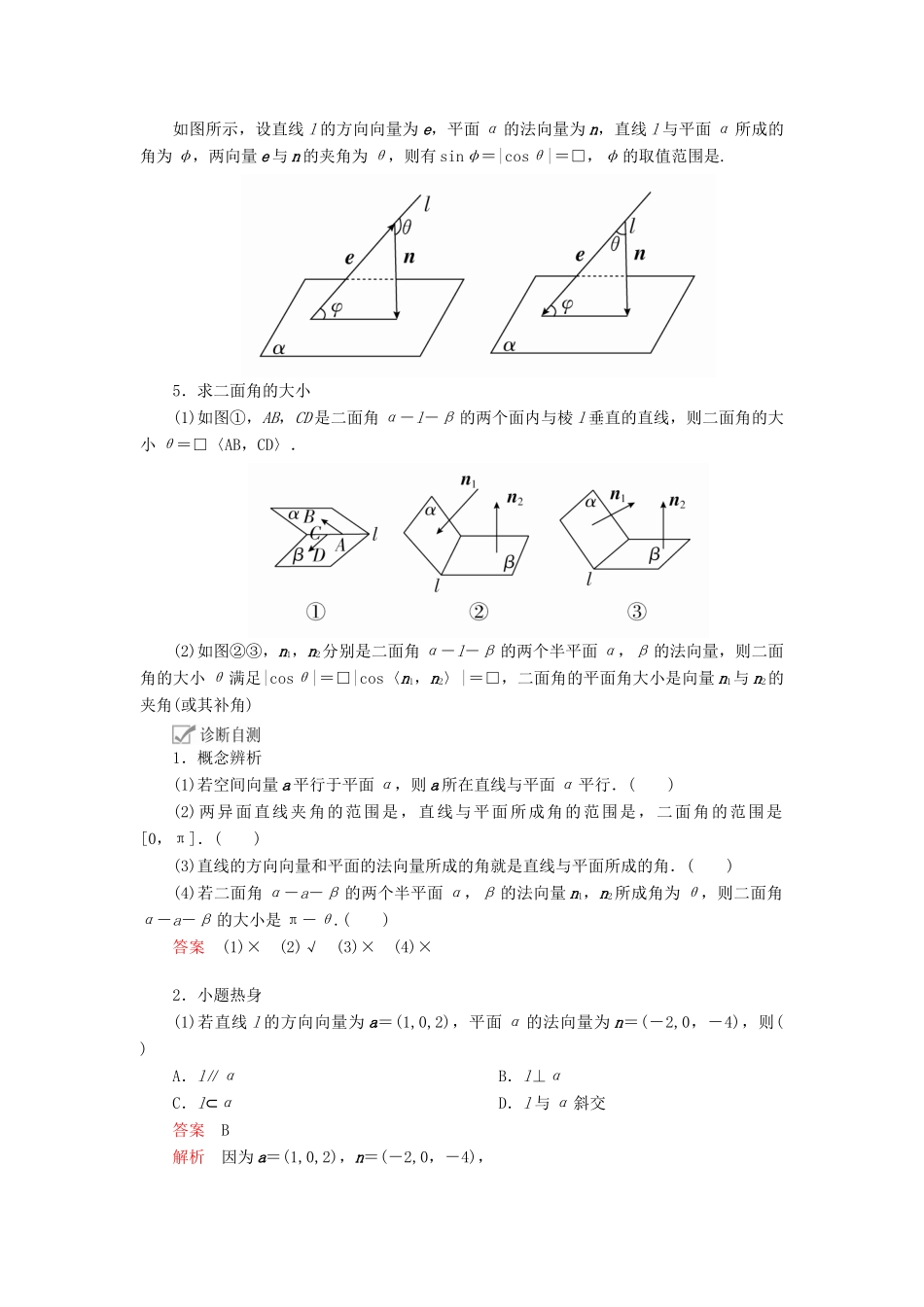
第7讲立体几何中的向量方法[考纲解读]1.理解直线的方向向量及平面的法向量,并能用向量语言表述线线、线面、面面的平行和垂直关系.(重点)2.能用向量方法证明立体几何中有关线面位置关系的一些简单定理,并能用向量方法解决线线、线面、面面的夹角的计算问题.(难点)[考向预测]从近三年高考情况来看,本讲为高考必考内容.预测2020年高考将会以空间向量为工具,证明平行与垂直以及求空间角的计算问题.试题以解答题的形式呈现,难度为中等偏上.1.用向量证明空间中的平行关系(1)设直线l1和l2的方向向量分别为v1和v2,则l1∥l2(或l1与l2重合)⇔□v1∥v2⇔v1=λv2.(2)设直线l的方向向量为v,与平面α共面的两个不共线向量v1和v2,则l∥α或l⊂α⇔存在两个实数x,y,使v=□xv1+yv2.(3)设直线l的方向向量为v,平面α的法向量为u,则l∥α或l⊂α⇔□v⊥u⇔□v·u=0.(4)设平面α和β的法向量分别为u1,u2,则α∥β⇔□u1∥u2⇔u1=λu2.2.用向量证明空间中的垂直关系(1)设直线l1和l2的方向向量分别为v1和v2,则l1⊥l2⇔□v1⊥v2⇔□v1·v2=0.(2)设直线l的方向向量为v,平面α的法向量为u,则l⊥α⇔□v∥u⇔□v=λu.(3)设平面α和β的法向量分别为u1和u2,则α⊥β⇔□u1⊥u2⇔□u1·u2=0.3.两条异面直线所成角的求法设a,b分别是两异面直线l1,l2的方向向量,则4.直线和平面所成角的求法如图所示,设直线l的方向向量为e,平面α的法向量为n,直线l与平面α所成的角为φ,两向量e与n的夹角为θ,则有sinφ=|cosθ|=□,φ的取值范围是.5.求二面角的大小(1)如图①,AB,CD是二面角α-l-β的两个面内与棱l垂直的直线,则二面角的大小θ=□〈AB,CD〉.(2)如图②③,n1,n2分别是二面角α-l-β的两个半平面α,β的法向量,则二面角的大小θ满足|cosθ|=□|cos〈n1,n2〉|=□,二面角的平面角大小是向量n1与n2的夹角(或其补角)1.概念辨析(1)若空间向量a平行于平面α,则a所在直线与平面α平行.()(2)两异面直线夹角的范围是,直线与平面所成角的范围是,二面角的范围是[0,π].()(3)直线的方向向量和平面的法向量所成的角就是直线与平面所成的角.()(4)若二面角α-a-β的两个半平面α,β的法向量n1,n2所成角为θ,则二面角α-a-β的大小是π-θ.()答案(1)×(2)√(3)×(4)×2.小题热身(1)若直线l的方向向量为a=(1,0,2),平面α的法向量为n=(-2,0,-4),则()A.l∥αB.l⊥αC.l⊂αD.l与α斜交答案B解析因为a=(1,0,2),n=(-2,0,-4),所以n=-2a,所以a∥n,所以l⊥α.(2)已知向量AB=(2,2,1),AC=(4,5,3),则平面ABC的单位法向量是()A.B.C.±D.±答案D解析设平面ABC的一个法向量是n=(x,y,z),则取z=1,得x=,y=-1.则n=,|n|=,故平面ABC的单位法向量是±.(3)在正三棱柱ABC-A1B1C1中,若AB=BB1,则AB1与C1B所成角的大小为()A.60°B.75°C.90°D.105°答案C解析取AC的中点D,建立如图所示的空间直角坐标系.设AB=a,则B,C1,A,B1,从而AB1=,C1B=.所以cos〈AB1,C1B〉==0,所以AB1与C1B所成的角为90°.故选C.(4)在长方体ABCD-A1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1所成角的正弦值为________,二面角B-A1C1-D1的余弦值为________.答案-解析如图,建立空间直角坐标系Dxyz,则D1(0,0,1),C1(0,2,1),A1(1,0,1),B(1,2,0),∴D1C1=(0,2,0),A1C1=(-1,2,0),A1B=(0,2,-1),设平面A1BC1的一个法向量为n=(x,y,z),由即令y=1,得n=(2,1,2),设D1C1与平面A1BC1所成角为θ,则sinθ=|cos〈D1C1,n〉|===,即直线D1C1与平面A1BC1所成角的正弦值为.易知平面A1C1D1的法向量m=(0,0,1),∴cos〈m,n〉===.由图可知,二面角B-A1C1-D1为钝角,故二面角B-A1C1-D1的余弦值为-.题型利用空间向量研究空间中的位置关系角度1利用空间向量证明平行与垂直问题1.(2018·青岛模拟)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=AB,B1C1綊BC,AA1⊥平面BAC.求证:(1)A1B1⊥平面AA1C;(2)AB1∥平面A1C1C.证明 AA1⊥平面BAC.∴AA1⊥AB,AA1⊥AC.又 AB=AC,BC=AB,∴∠CAB=90°...