（新课标）高考数学大一轮复习 立体几何的热点问题课时作业 理-人教版高三全册数学试题VIP免费

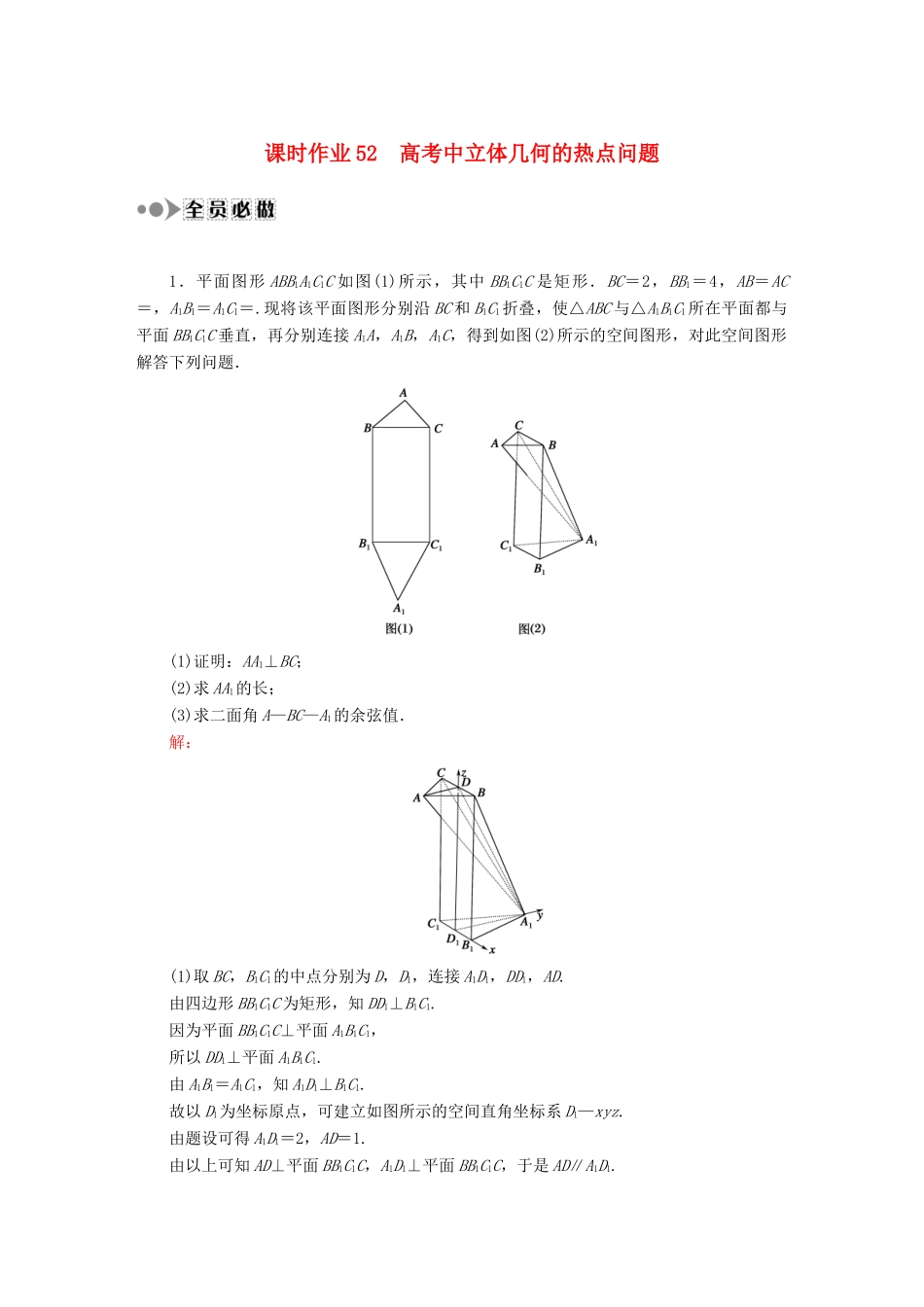
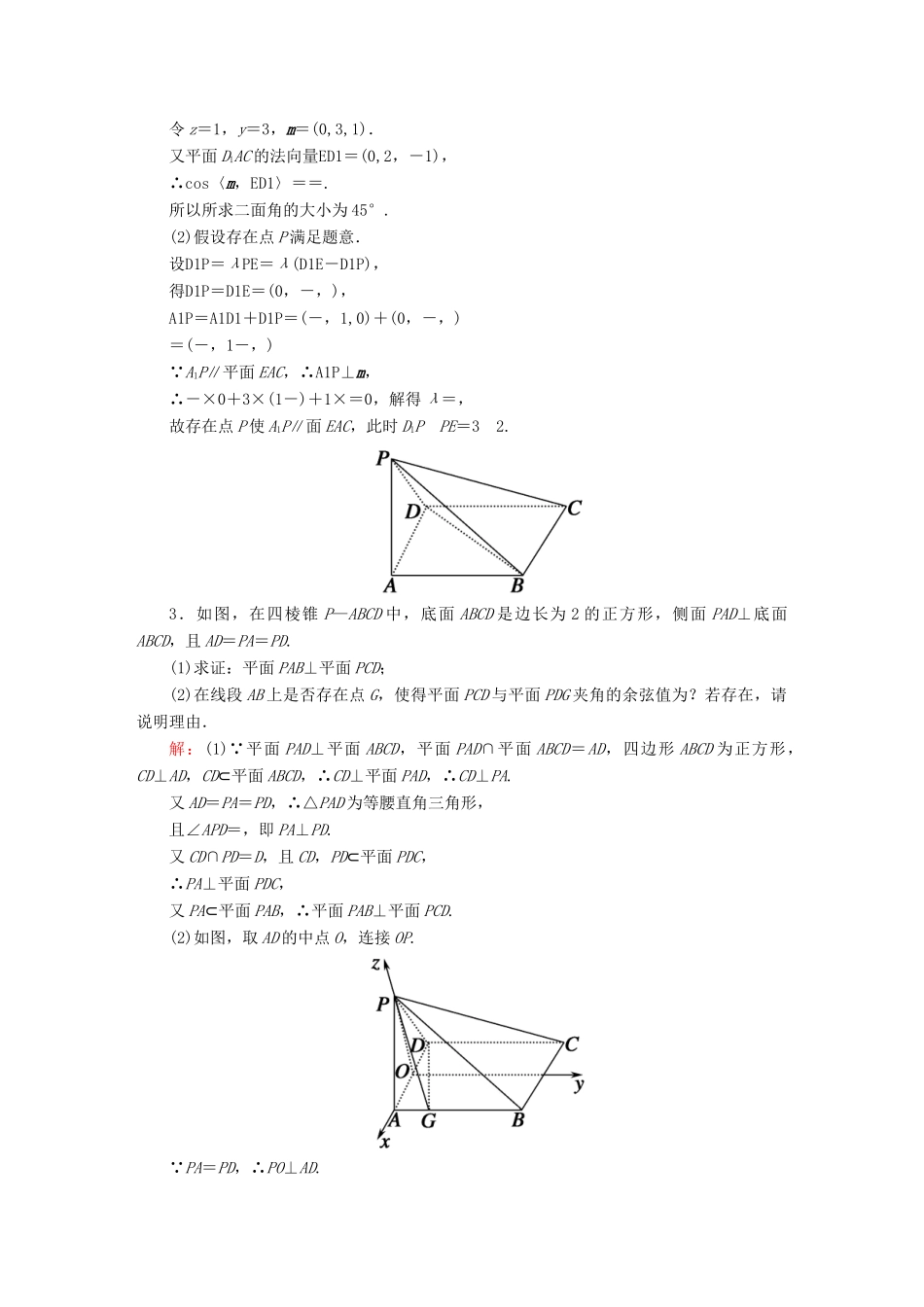
课时作业52高考中立体几何的热点问题1．平面图形ABB1A1C1C如图(1)所示，其中BB1C1C是矩形．BC＝2，BB1＝4，AB＝AC＝，A1B1＝A1C1＝.现将该平面图形分别沿BC和B1C1折叠，使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直，再分别连接A1A，A1B，A1C，得到如图(2)所示的空间图形，对此空间图形解答下列问题．(1)证明：AA1⊥BC；(2)求AA1的长；(3)求二面角A—BC—A1的余弦值．解：(1)取BC，B1C1的中点分别为D，D1，连接A1D1，DD1，AD.由四边形BB1C1C为矩形，知DD1⊥B1C1.因为平面BB1C1C⊥平面A1B1C1，所以DD1⊥平面A1B1C1.由A1B1＝A1C1，知A1D1⊥B1C1.故以D1为坐标原点，可建立如图所示的空间直角坐标系D1—xyz.由题设可得A1D1＝2，AD＝1.由以上可知AD⊥平面BB1C1C，A1D1⊥平面BB1C1C，于是AD∥A1D1.所以A(0，－1,4)，B(1,0,4)，A1(0,2,0)，C(－1,0,4)，D(0,0,4)．故AA1＝(0,3，－4)，BC＝(－2,0,0)，因为AA1·BC＝0，所以AA1⊥BC，即AA1⊥BC.(2)因为AA1＝(0,3，－4)，所以|AA1|＝5，即AA1＝5.(3)连接A1D.由BC⊥AD，BC⊥AA1，可知BC⊥面A1AD，BC⊥A1D，所以∠ADA1为二面角A—BC—A1的平面角．因为DA＝(0，－1,0)，DA1＝(0,2，－4)，所以cos〈DA，DA1〉＝＝－，即二面角A—BC—A1的余弦值为－.2．在如图所示的几何体中，底面ABCD为菱形，∠BAD＝60°，AA1綊DD1綊CC1∥BE，且AA1＝AB，D1E⊥平面D1AC，AA1⊥底面ABCD.(1)求二面角D1—AC—E的大小；(2)在D1E上是否存在一点P，使得A1P∥平面EAC，若存在，求的值，若不存在，说明理由．解：(1)设AC与BD交于O，如图所示建立空间直角坐标系O－xyz，设AB＝2，则A(，0,0)，B(0，－1,0)，C(－，0,0)，D(0,1,0)，D1(0,1,2)，设E(0，－1，t)，t>0，则ED1＝(0,2,2－t)，CA＝(2，0,0)，D1A＝(，－1，－2)． D1E⊥面D1AC，∴D1E⊥CA，D1E⊥D1A，∴解得t＝3，∴E(0，－1,3)，∴AE＝(－，－1,3)，设平面EAC的法向量为m＝(x，y，z)，则∴令z＝1，y＝3，m＝(0,3,1)．又平面D1AC的法向量ED1＝(0,2，－1)，∴cos〈m，ED1〉＝＝.所以所求二面角的大小为45°.(2)假设存在点P满足题意．设D1P＝λPE＝λ(D1E－D1P)，得D1P＝D1E＝(0，－，)，A1P＝A1D1＋D1P＝(－，1,0)＋(0，－，)＝(－，1－，) A1P∥平面EAC，∴A1P⊥m，∴－×0＋3×(1－)＋1×＝0，解得λ＝，故存在点P使A1P∥面EAC，此时D1PPE＝32.3．如图，在四棱锥P—ABCD中，底面ABCD是边长为2的正方形，侧面PAD⊥底面ABCD，且AD＝PA＝PD.(1)求证：平面PAB⊥平面PCD；(2)在线段AB上是否存在点G，使得平面PCD与平面PDG夹角的余弦值为？若存在，请说明理由．解：(1) 平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，四边形ABCD为正方形，CD⊥AD，CD⊂平面ABCD，∴CD⊥平面PAD，∴CD⊥PA.又AD＝PA＝PD，∴△PAD为等腰直角三角形，且∠APD＝，即PA⊥PD.又CD∩PD＝D，且CD，PD⊂平面PDC，∴PA⊥平面PDC，又PA⊂平面PAB，∴平面PAB⊥平面PCD.(2)如图，取AD的中点O，连接OP. PA＝PD，∴PO⊥AD. 侧面PAD⊥底面ABCD，平面PAD∩平面ABCD＝AD，∴PO⊥平面ABCD， AD＝PA＝PD，∴PA⊥PD，OP＝OA＝1.以O为原点，直线OA，OP分别为x，z轴，且底面ABCD中过O点垂直于AD的直线为y轴建立空间直角坐标系，则A(1,0,0)，D(－1,0,0)，P(0,0,1)．假设在AB上存在点G使得平面PCD与平面PDG夹角的余弦值为，连接PG，DG.设G(1，a,0)(0≤a≤2)．由(1)知平面PCD的一个法向量为PA＝(1,0，－1)．设平面PDG的法向量为n＝(x，y，z)． DP＝(1,0,1)，GD＝(－2，－a,0)，∴由n·DP＝0，n·GD＝0可得，令x＝1，则y＝－，z＝－1，故n＝(1，－，－1)，∴cos〈n，PA〉＝＝＝＝，解得，a＝.∴在线段AB上存在点G(1，，0)，使得平面PCD与平面PDG夹角的余弦值为.1．(2014·安徽卷)如右图，四棱柱ABCD—A1B1C1D1中，A1A⊥底面ABCD，四边形ABCD为梯形，AD∥BC，且AD＝2BC.过A1，C，D三点的平面记为α，BB1与α的交点为Q.(1)证明：Q为BB1的中点；(2)求此四棱柱被平面α所分成上下两部分的体积之比；(3)若A1A＝4，CD＝2，梯形ABCD的面积为6，求平面α与底面ABCD所成二面角的大小．解：(1)因为BQ∥AA1，BC∥AD，BC∩BQ＝B，AD∩AA1＝A.所以平面QBC∥平面A1AD.从...