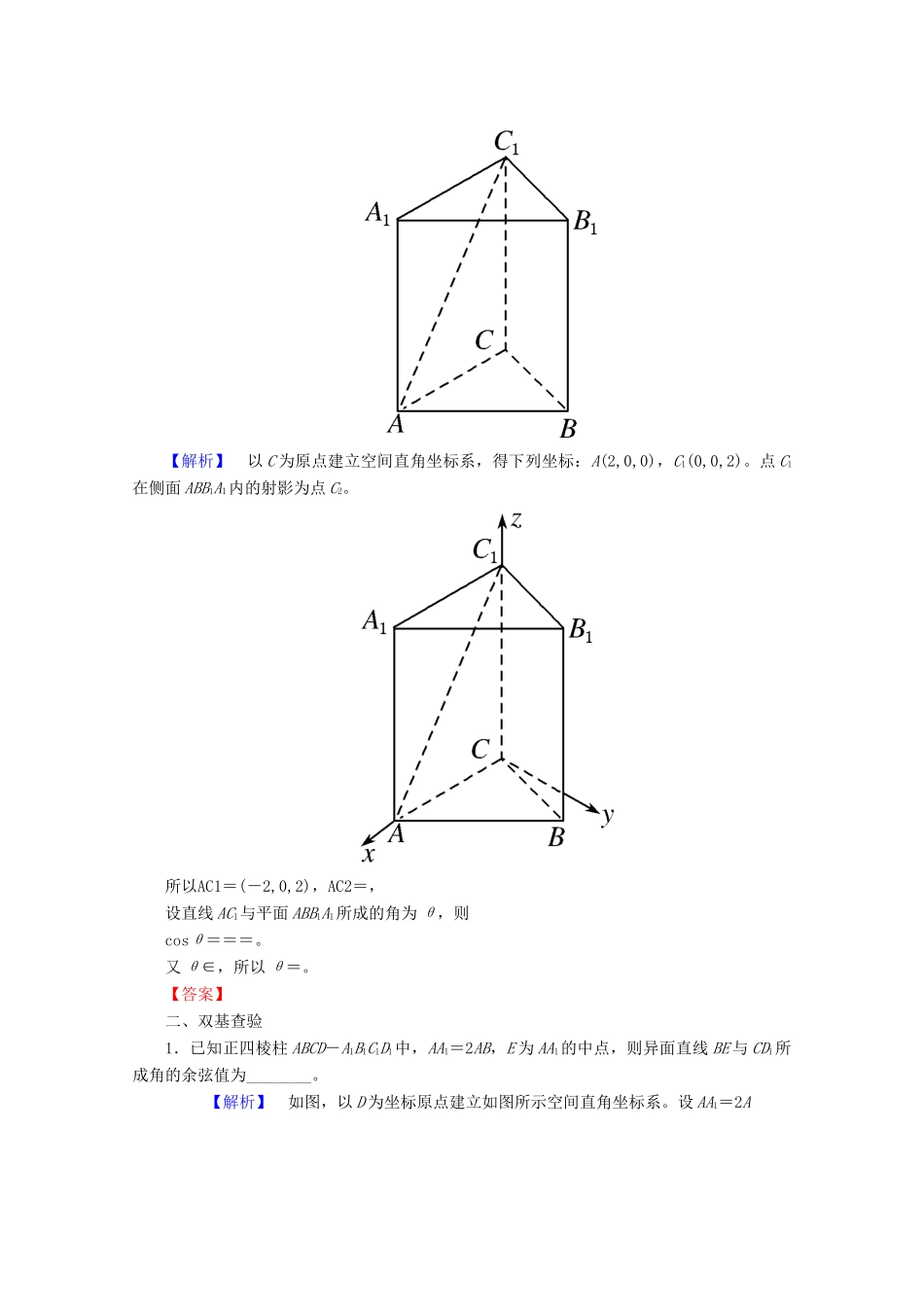
第七节立体几何中的向量方法☆☆☆2017考纲考题考情☆☆☆考纲要求真题举例命题角度能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题,了解向量方法在研究立体几何中的应用。2016,全国卷Ⅰ,18,12分(面面垂直、二面角)2016,全国卷Ⅱ,19,12分(线面垂直,二面角)2016,全国卷Ⅲ,19,12分(线面平行、线面角)2016,天津卷,17,13分(线面平行,线面角、二面角)2016,山东卷,17,12分(线面平行、二面角)1.本节是高考中的必考内容,涉及用向量法计算空间异面直线所成角、直线和平面所成角、二面角;2.题型以解答题为主,要求有较强的运算能力,广泛应用函数与方程的思想,转化与化归思想。微知识小题练自|主|排|查1.两条异面直线所成角的求法设两条异面直线a,b的方向向量为a,b,其夹角为θ,则cosφ=|cosθ|=(其中φ为异面直线a,b所成的角)。2.直线和平面所成角的求法如图所示,设直线l的方向向量为e,平面α的法向量为n,直线l与平面α所成的角为φ,向量e与n的夹角为θ,则有sinφ=|cosθ|=。3.求二面角的大小(1)如图①,AB,CD是二面角αlβ的两个面内与棱l垂直的直线,则二面角的大小θ=〈AB,CD〉。(2)如图②③,n1,n2分别是二面角αlβ的两个半平面α,β的法向量,则二面角的大小θ=〈n1,n2〉或π-〈n1,n2〉。微点提醒1.一般来说,如果已知的空间几何体中含有两两垂直且交于一点的三条直线时,就以这三条直线为坐标轴建立空间直角坐标系;如果不存在这样的三条直线,则应尽可能找两条垂直相交的直线,以其为两条坐标轴建立空间直角坐标系,即坐标系建立时以其中的垂直相交直线为基本出发点。2.异面直线所成的角与其方向向量的夹角:当异面直线的方向向量的夹角为锐角或直角时,就是该异面直线的夹角;否则向量夹角的补角是异面直线所成的角。3.二面角与法向量的夹角:利用平面的法向量求二面角的大小时,当求出两半平面α,β的法向量n1,n2时,要根据向量坐标在图形中观察法向量的方向,从而确定二面角与向量n1,n2的夹角是相等,还是互补。小|题|快|练一、走进教材(选修2-1P117T4改编)正三棱柱(底面是正三角形的直棱柱)ABC-A1B1C1的底面边长为2,侧棱长为2,则AC1与侧面ABB1A1所成的角为________。【解析】以C为原点建立空间直角坐标系,得下列坐标:A(2,0,0),C1(0,0,2)。点C1在侧面ABB1A1内的射影为点C2。所以AC1=(-2,0,2),AC2=,设直线AC1与平面ABB1A1所成的角为θ,则cosθ===。又θ∈,所以θ=。【答案】二、双基查验1.已知正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为AA1的中点,则异面直线BE与CD1所成角的余弦值为________。【解析】如图,以D为坐标原点建立如图所示空间直角坐标系。设AA1=2AB=2,则B(1,1,0),E(1,0,1),C(0,1,0),D1(0,0,2),所以BE=(0,-1,1),CD1=(0,-1,2),所以cos〈BE,CD1〉==。【答案】2.过正方形ABCD的顶点A作线段PA⊥平面ABCD,如果AB=PA,那么平面ABP与平面CDP所成的二面角的大小为________。【解析】建立如图所示空间直角坐标系,设AB=PA=1,知A(0,0,0),B(1,0,0),D(0,1,0),C(1,1,0),P(0,0,1),由题意,AD⊥平面ABP,设E为PD的中点,连接AE,则AE⊥PD,又因为CD⊥平面PAD,所以AE⊥CD,又PD∩CD=D,所以AE⊥平面CDP。所以AD=(0,1,0),AE=分别是平面ABP,平面CDP的法向量,且〈AD,AE〉=45°,所以平面ABP与平面CDP所成的二面角为45°。【答案】45°第一课时利用空间向量求空间角微考点大课堂考点一异面直线所成的角【典例1】(2015·全国卷Ⅰ)如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC。(1)证明:平面AEC⊥平面AFC;(2)求直线AE与直线CF所成角的余弦值。【解析】(1)证明:如图,连接BD,设BD∩AC=G,连接EG,FG,EF。在菱形ABCD中,不妨设GB=1。由∠ABC=120°,可得AG=GC=。由BE⊥平面ABCD,AB=BC,可知AE=EC。又AE⊥EC,所以EG=,且EG⊥AC。在Rt△EBG中,可得BE=,故DF=。在Rt△FDG中,可得FG=。在直角梯形BDFE中,由BD=2,BE=,DF=,可得EF=。从而EG2+FG2=EF2,所以EG⊥FG...