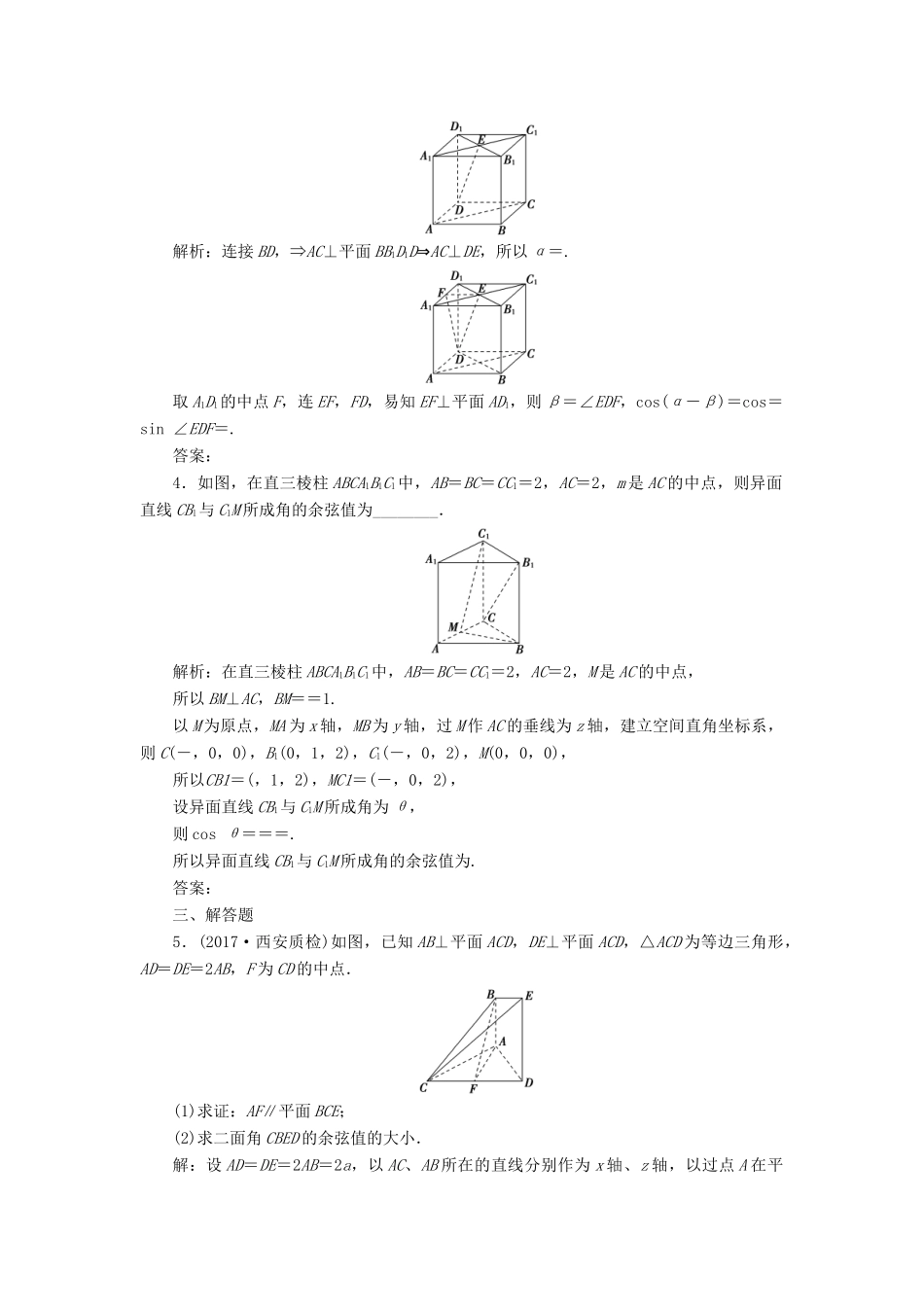
第3讲圆锥曲线的综合问题一、选择题1.在三棱柱ABCA1B1C1中,底面是边长为1的正三角形,侧棱AA1⊥底面ABC,点D在棱BB1上,且BD=1,若AD与平面AA1C1C所成的角为α,则sinα的值是()A.B.C.D.解析:如图,建立空间直角坐标系,易求点D.平面AA1C1C的一个法向量是n=(1,0,0),所以cos〈n,AD〉==,则sinα=.答案:D2.在三棱锥PABC中,侧面PAC与底面ABC均是等腰直角三角形.O是斜边AC的中点,平面PAC⊥平面ABC,且AC=4,设θ是二面角PABC的大小,则sinθ=()(导学号54850122)A.B.C.D.解析:连接PO,过O作OD⊥AB,连接PD(如图).因为平面PAC⊥平面ABC,PO⊥AC,所以PO⊥平面ABC,PO⊥AB.又OD⊥AB.从而AB⊥平面POD,PD⊥AB,所以∠PDO为二面角PABC的平面角,即θ=∠PDO.由题设,OD=BC=×2=,OP=2,所以PD==.故sinθ=sin∠PDO===.答案:C二、填空题3.(2017·衡阳联考)如图所示,在正方体AC1中,AB=2,A1C1∩B1D1=E,直线AC与直线DE所成的角为α,直线DE与平面BCC1B1所成的角为β,则cos(α-β)=________.解析:连接BD,⇒AC⊥平面BB1D1D⇒AC⊥DE,所以α=.取A1D1的中点F,连EF,FD,易知EF⊥平面AD1,则β=∠EDF,cos(α-β)=cos=sin∠EDF=.答案:4.如图,在直三棱柱ABCA1B1C1中,AB=BC=CC1=2,AC=2,m是AC的中点,则异面直线CB1与C1M所成角的余弦值为________.解析:在直三棱柱ABCA1B1C1中,AB=BC=CC1=2,AC=2,M是AC的中点,所以BM⊥AC,BM==1.以M为原点,MA为x轴,MB为y轴,过M作AC的垂线为z轴,建立空间直角坐标系,则C(-,0,0),B1(0,1,2),C1(-,0,2),M(0,0,0),所以CB1=(,1,2),MC1=(-,0,2),设异面直线CB1与C1M所成角为θ,则cosθ===.所以异面直线CB1与C1M所成角的余弦值为.答案:三、解答题5.(2017·西安质检)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.(1)求证:AF∥平面BCE;(2)求二面角CBED的余弦值的大小.解:设AD=DE=2AB=2a,以AC、AB所在的直线分别作为x轴、z轴,以过点A在平面ACD上作出以AC垂直的直线作为y轴,建立如图所示的坐标系,A(0,0,0),C(2a,0,0),B(0,0,a),D(a,a,0),E(a,a,2a).因为F为CD的中点,所以F.(1)证明:AF=,BE=(a,a,a),BC=(2a,0,-a),所以AF=(BE+BC),AF⊄平面BCE,所以AF∥平面BCE.(2)设平面BCE的法向量m=(x,y,z),则即不妨令x=1可得m=(1,-,2).设平面BDE的法向量n=(x0,y0,z0),则即令x0=可得n=(,-1,0).于是cos〈m,n〉==.故二面角CBED的余弦值为.6.(2017·德州二模)如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.(1)求证:BD⊥平面ADG;(2)求直线GB与平面AEFG所成角的正弦值.(1)证明:在△BAD中,因为AB=2AD=2,∠BAD=60°.由余弦定理,BD2=AD2+AB2-2AB·ADcos60°,BD=,因为AB2=AD2+DB2,所以AD⊥DB,在直平行六面体中,GD⊥平面ABCD,DB⊂平面ABCD,所以GD⊥DB,又AD∩GD=D,所以BD⊥平面ADG.(2)解:如图以D为原点建立空间直角坐标系Dxyz,因为∠BAE=∠GAD=45°,AB=2AD=2,所以A(1,0,0),B(0,,0),E(0,,2),G(0,0,1),AE=(-1,,2),AG=(-1,0,1),GB=(0,,-1).设平面AEFG的法向量n=(x,y,z),令x=1,得y=,z=1,所以n=.设直线GB和平面AEFG的夹角为θ,所以sinθ=|cos〈GB,n〉|==,所以直线GB与平面AEFG所成角的正弦值为.7.(2016·北京卷)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=.(导学号54850123)(1)求证:PD⊥平面PAB;(2)求直线PB与平面PCD所成角的正弦值;(3)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求的值;若不存在,说明理由.(1)证明:因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,AB⊥AD,所以AB⊥平面PAD,所以AB⊥PD.又PA⊥PD,AB∩PA=A,所以PD⊥平面PAB.(2)解:取AD的中点O,连接PO,CO.因为PA=PD,所以PO⊥AD.因为PO⊂平面PAD,平面PAD⊥平面ABCD.所以PO⊥平面ABCD.因为CO⊂平面ABCD,...