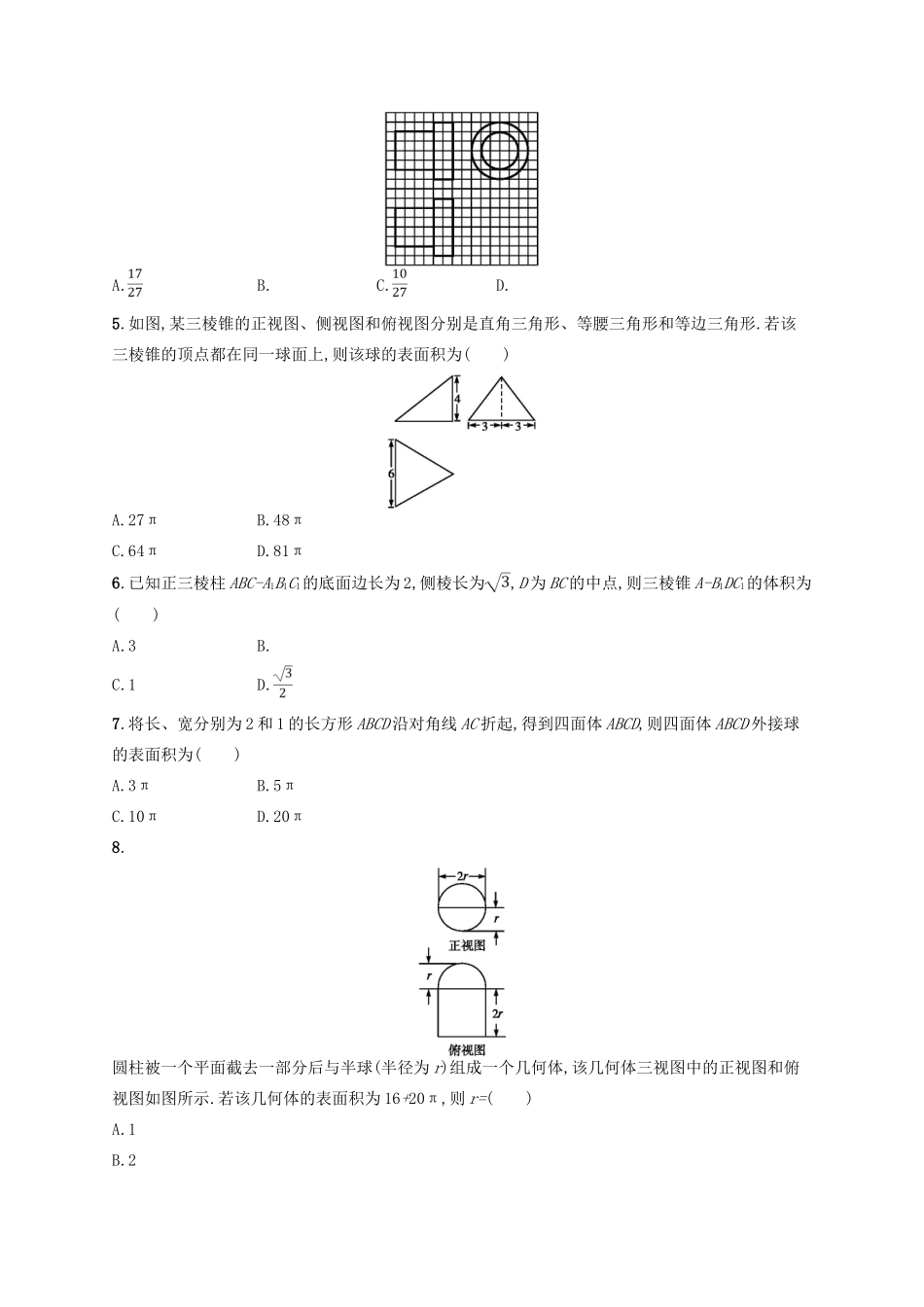
专题对点练185.1~5.3组合练(限时90分钟,满分100分)一、选择题(共9小题,满分45分)1.某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是()A.+1B.+3C.+1D.+32.(2018全国名校大联考第四次联考)已知α,β是相异两平面,m,n是相异两直线,则下列命题错误的是()A.若m∥n,m⊥α,则n⊥αB.若m⊥α,m⊥β,则α∥βC.若m⊥α,m∥β,则α⊥βD.若m∥α,α∩β=n,则m∥n3.某几何体的三视图如图所示,则该几何体中,面积最大的侧面的面积为()A.B.C.D.34.如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为()A.B.C.D.5.如图,某三棱锥的正视图、侧视图和俯视图分别是直角三角形、等腰三角形和等边三角形.若该三棱锥的顶点都在同一球面上,则该球的表面积为()A.27πB.48πC.64πD.81π6.已知正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为,D为BC的中点,则三棱锥A-B1DC1的体积为()A.3B.C.1D.7.将长、宽分别为2和1的长方形ABCD沿对角线AC折起,得到四面体ABCD,则四面体ABCD外接球的表面积为()A.3πB.5πC.10πD.20π8.圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=()A.1B.2C.4D.89.(2018全国Ⅲ,文12)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9,则三棱锥D-ABC体积的最大值为()A.12B.18C.24D.54二、填空题(共3小题,满分15分)10.(2018天津,文11)如图,已知正方体ABCD-A1B1C1D1的棱长为1,则四棱锥A1-BB1D1D的体积为.11.已知三棱锥A-BCD,AB=AC=BC=2,BD=CD=,点E是BC的中点,点A在平面BCD上的射影恰好为DE的中点F,则该三棱锥外接球的表面积为.12.已知四面体ABCD,AB=4,AC=AD=6,∠BAC=∠BAD=60°,∠CAD=90°,则该四面体外接球的半径为.三、解答题(共3个题,满分分别为13分,13分,14分)13.如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥平面ABCD,BC=AP=5,AB=3,AC=4,M,N分别在线段AD,CP上,且=4.(1)求证:MN∥平面PAB;(2)求三棱锥P-AMN的体积.14.在如图所示的五面体ABCDEF中,矩形BCEF所在的平面与平面ABC垂直,AD∥CE,CE=2AD=2,M是BC的中点,在△ABC中,∠BAC=60°,AB=2AC=2.求证:(1)AM∥平面BDE;(2)DE⊥平面BDC,并求三棱锥C-DBE的体积.15.如图①,在边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点.将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A',连接EF,A'B,如图②.(1)求异面直线A'D与EF所成角的大小;(2)求三棱锥D-A'EF的体积.专题对点练18答案1.A解析V=×3××π×12++1,故选A.2.D解析由线面垂直的性质可知选项A,B,C正确.如图所示,对于选项D,在正方体ABCD-A1B1C1D1中,取直线m为AD,平面α为上底面A1B1C1D1,平面β为平面CDD1C1,则直线n为C1D1,此时有m∥α,α∩β=n,直线m与n为异面直线,即选项D错误.故选D.3.B解析由三视图可知,几何体的直观图如图所示,平面AED⊥平面BCDE,四棱锥A-BCDE的高为1,四边形BCDE是边长为1的正方形,则S△AED=×1×1=,S△ABC=S△ABE=×1×,S△ACD=×1×,故选B.4.C解析由零件的三视图可知,该几何体为两个圆柱组合而成,如图所示.切削掉部分的体积V1=π×32×6-π×22×4-π×32×2=20π(cm3),原来毛坯体积V2=π×32×6=54π(cm3).故所求比值为.5.C解析由三视图可知,该几何体为三棱锥,三棱锥的高VA=4,直观图如图所示. △ABC是边长为6的等边三角形,∴外接球的球心D在底面ABC的投影为△ABC的中心O,过D作DE⊥VA于E,则E为VA的中点,连接OA,DA,则DE=OA=×3=2,AE=VA=2,DA为外接球的半径r,∴r==4,∴该球的表面积S=4πr2=64π.故选C.6.C解析 D是等边三角形ABC的边BC的中点,∴AD⊥BC.又ABC-A1B1C1为正三棱柱,∴AD⊥平面BB1C1C. 四边形BB1C1C为矩形,∴×2×.又AD=2×,∴·AD=×=1.故选C.7.B解析由题意可知,直角三角形斜边的中线是斜边的一半,所以长、宽分别为2和1的长方形ABCD沿对角线AC折起二面角,得到四面体ABCD,则四面体ABCD的外接球的球心O为AC的中点,半径R=,所求四面体ABCD的外接球的表面积为4π×=5π.故选B.8.B解析由条件及几何体的三视...