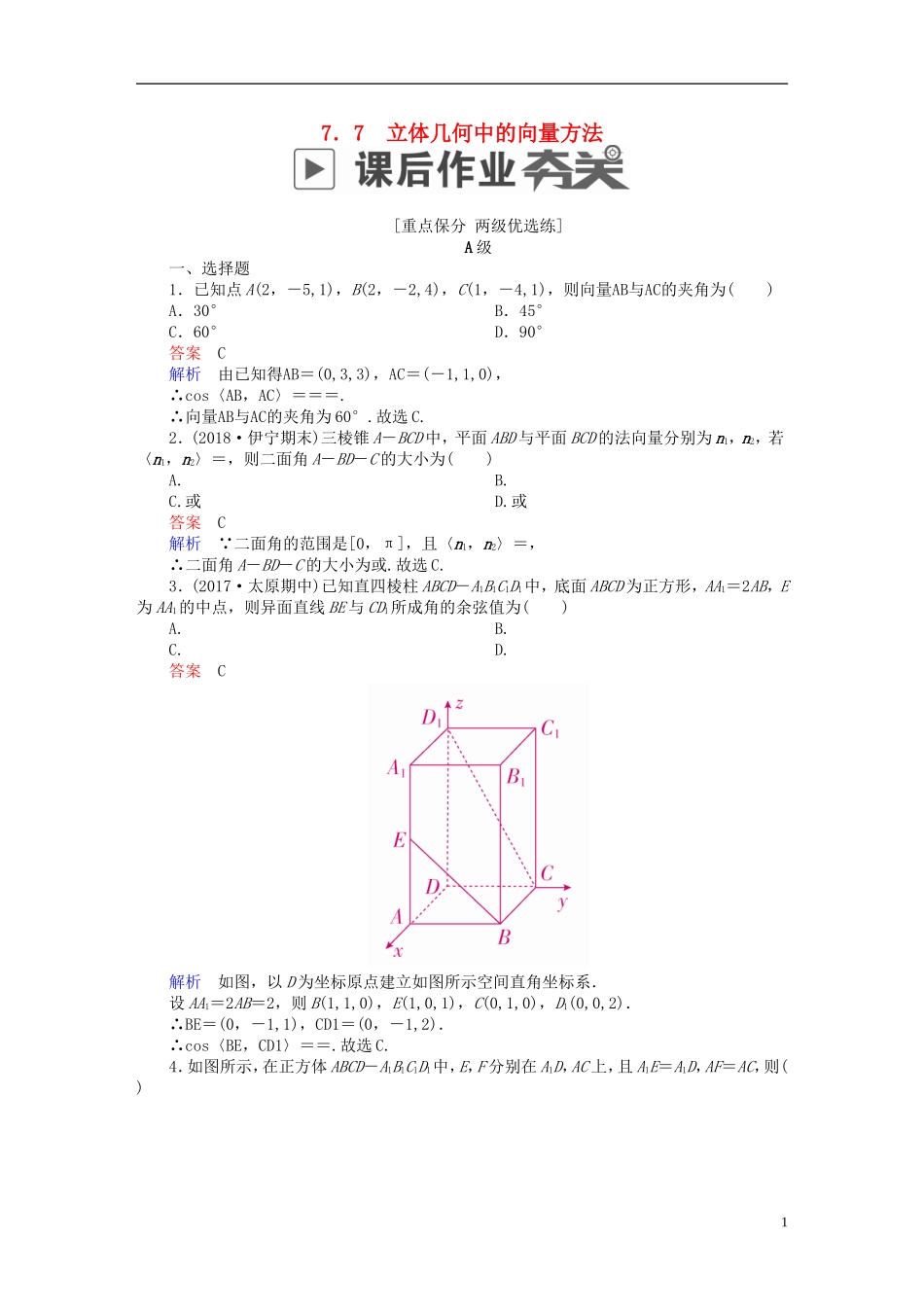
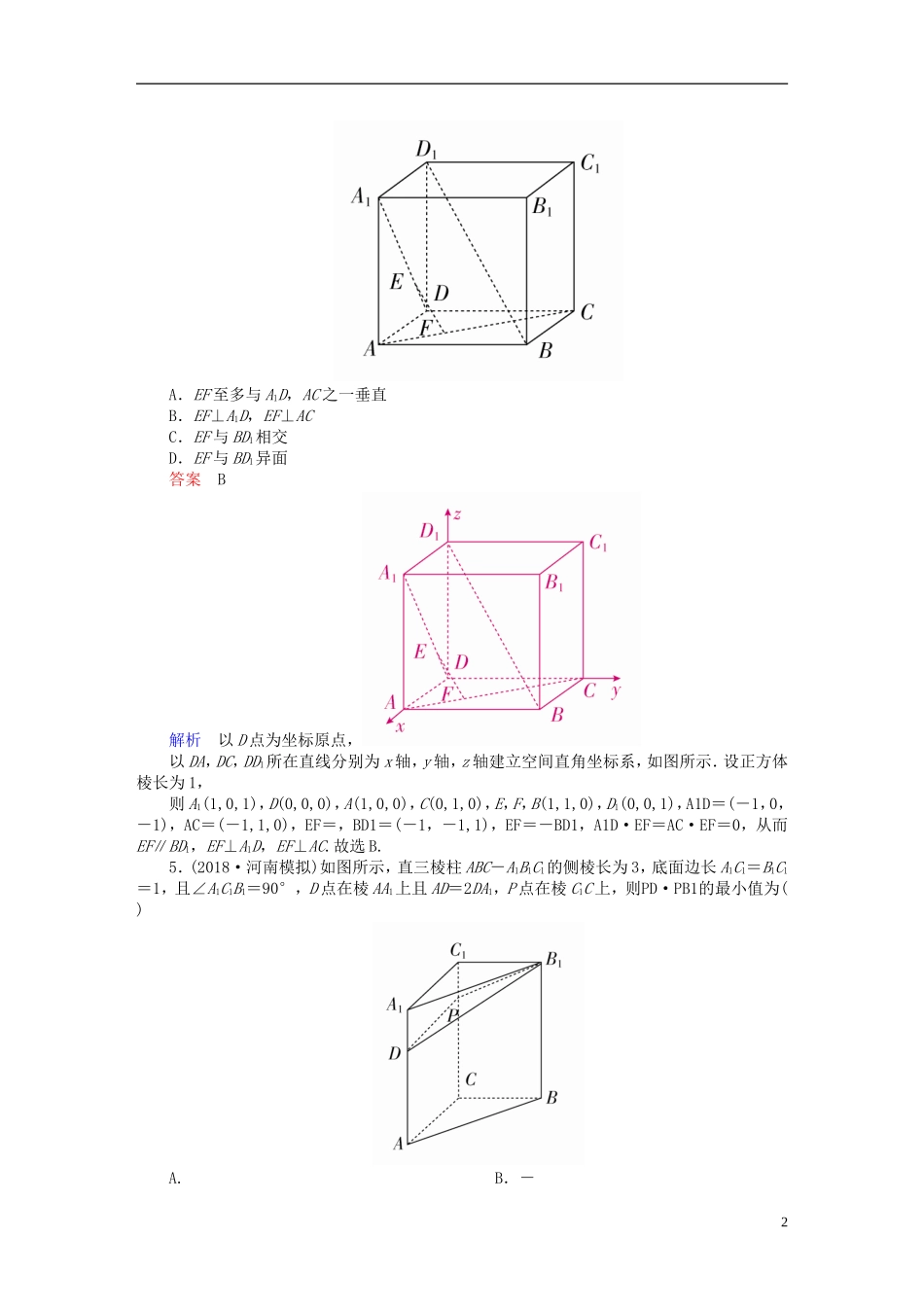
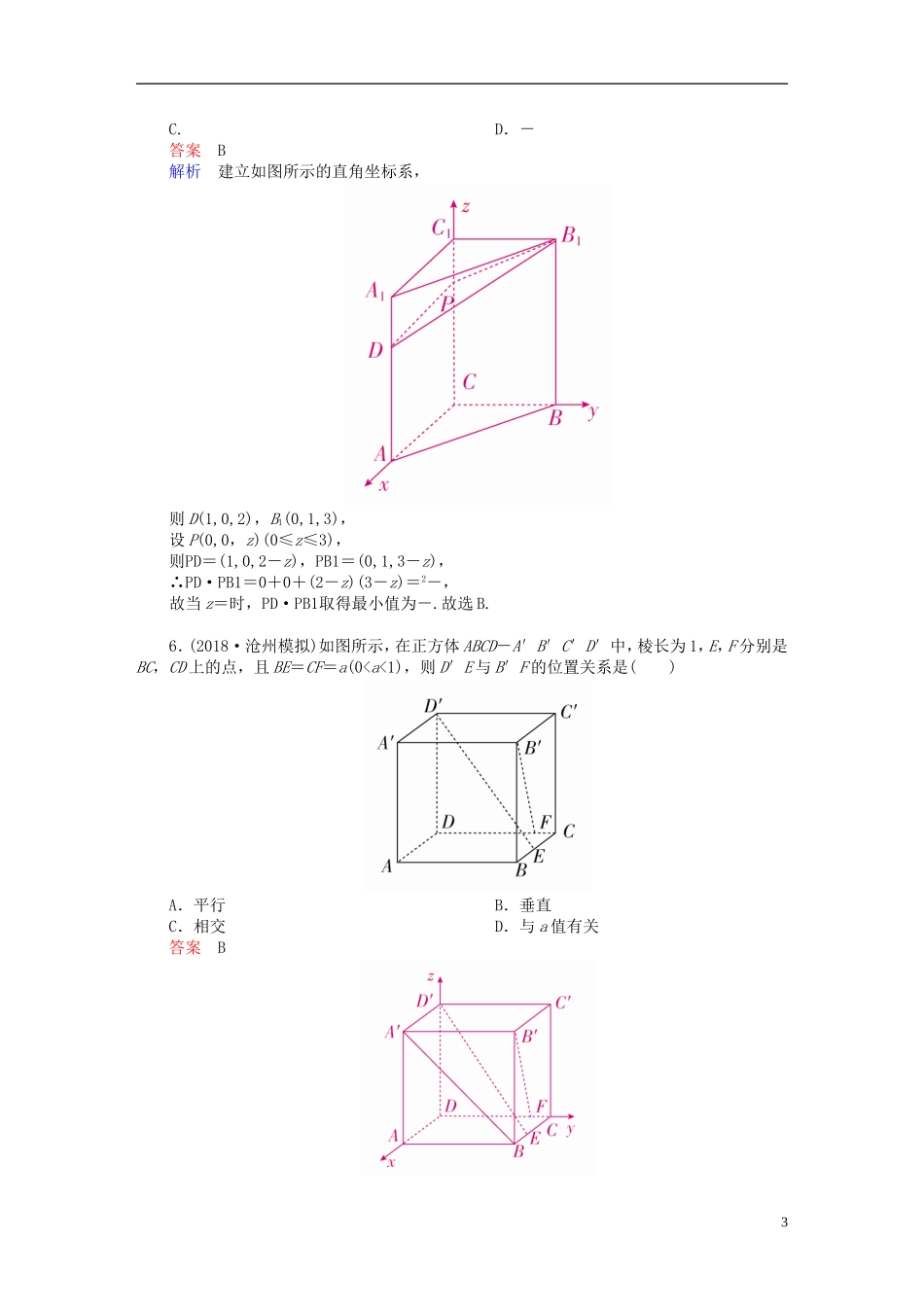
7.7立体几何中的向量方法[重点保分两级优选练]A级一、选择题1.已知点A(2,-5,1),B(2,-2,4),C(1,-4,1),则向量AB与AC的夹角为()A.30°B.45°C.60°D.90°答案C解析由已知得AB=(0,3,3),AC=(-1,1,0),∴cos〈AB,AC〉===.∴向量AB与AC的夹角为60°.故选C.2.(2018·伊宁期末)三棱锥A-BCD中,平面ABD与平面BCD的法向量分别为n1,n2,若〈n1,n2〉=,则二面角A-BD-C的大小为()A.B.C.或D.或答案C解析 二面角的范围是[0,π],且〈n1,n2〉=,∴二面角A-BD-C的大小为或.故选C.3.(2017·太原期中)已知直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,E为AA1的中点,则异面直线BE与CD1所成角的余弦值为()A.B.C.D.答案C解析如图,以D为坐标原点建立如图所示空间直角坐标系.设AA1=2AB=2,则B(1,1,0),E(1,0,1),C(0,1,0),D1(0,0,2).∴BE=(0,-1,1),CD1=(0,-1,2).∴cos〈BE,CD1〉==.故选C.4.如图所示,在正方体ABCD-A1B1C1D1中,E,F分别在A1D,AC上,且A1E=A1D,AF=AC,则()1A.EF至多与A1D,AC之一垂直B.EF⊥A1D,EF⊥ACC.EF与BD1相交D.EF与BD1异面答案B解析以D点为坐标原点,以DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图所示.设正方体棱长为1,则A1(1,0,1),D(0,0,0),A(1,0,0),C(0,1,0),E,F,B(1,1,0),D1(0,0,1),A1D=(-1,0,-1),AC=(-1,1,0),EF=,BD1=(-1,-1,1),EF=-BD1,A1D·EF=AC·EF=0,从而EF∥BD1,EF⊥A1D,EF⊥AC.故选B.5.(2018·河南模拟)如图所示,直三棱柱ABC-A1B1C1的侧棱长为3,底面边长A1C1=B1C1=1,且∠A1C1B1=90°,D点在棱AA1上且AD=2DA1,P点在棱C1C上,则PD·PB1的最小值为()A.B.-2C.D.-答案B解析建立如图所示的直角坐标系,则D(1,0,2),B1(0,1,3),设P(0,0,z)(0≤z≤3),则PD=(1,0,2-z),PB1=(0,1,3-z),∴PD·PB1=0+0+(2-z)(3-z)=2-,故当z=时,PD·PB1取得最小值为-.故选B.6.(2018·沧州模拟)如图所示,在正方体ABCD-A′B′C′D′中,棱长为1,E,F分别是BC,CD上的点,且BE=CF=a(0