高中数学 课时作业15 第十一章 立体几何 11.1.6 祖暅原理与几何体的体积（含解析）新人教B版必修第四册-新人教B版高一第四册数学试题VIP免费

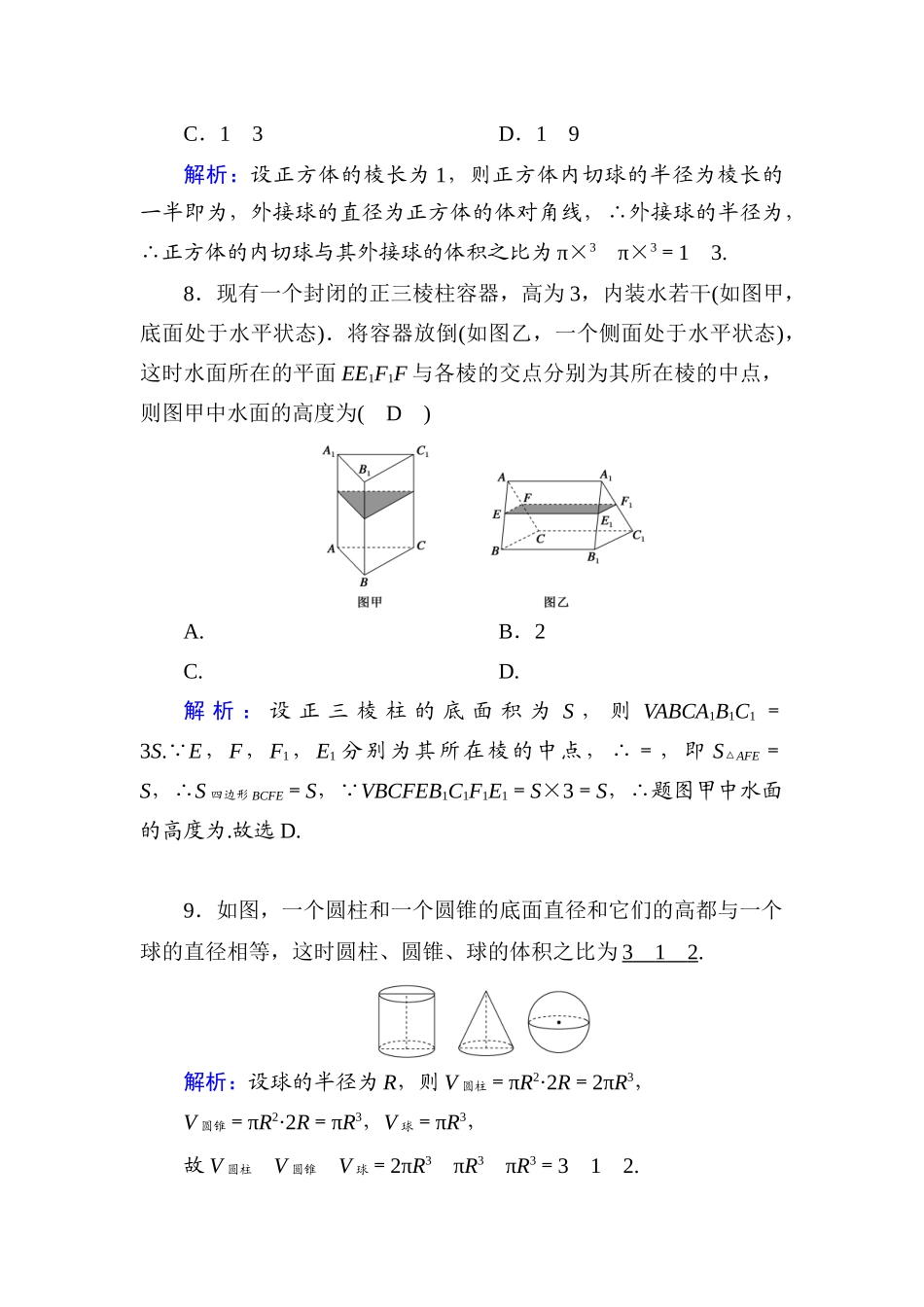
课时作业15祖暅原理与几何体的体积时间：45分钟1．将两个棱长为10cm的正方体铜块熔化后铸成底面边长为5cm的正四棱柱，则该四棱柱的高为(B)A．8cmB．80cmC．40cmD.cm解析：设正四棱柱的高为hcm，依题意得5×5×h＝2×103，解得h＝80(cm)．2．若一个圆锥的轴截面(过圆锥顶点和底面直径的截面)是等边三角形，其面积为，则这个圆锥的体积为(B)A．3πB.πC.πD.π解析：设圆锥的底面半径为R，依题意知该圆锥的高即轴截面的高h＝×2R＝R，所以×2R×R＝，解得R＝1.所以V圆锥＝×π×12×＝π.3.圆台上、下底面面积分别为π、4π，侧面积为6π，则这个圆台的体积为(A)A.πB.πC．2πD.π解析：设圆台的上、下底面半径分别为r′、r，则πr′2＝π，πr2＝4π，∴r′＝1，r＝2，设母线长为l，π(1＋2)l＝6π，∴l＝2，∴高h＝＝.∴V圆台＝×(1＋22＋1×2)×＝π.4．已知正四棱台ABCDA′B′C′D′中，AB＝3，A′B′＝6，体积V＝126，则该正四棱台的高为(C)A．18B．9C．6D．12解析：设正四棱台的高为h，则有(32＋62＋)h＝126，解得h＝6，即该正四棱台的高为6，故选C.5．在棱长为1的正方体上，分别用过共顶点的三条棱中点的平面截该正方体，则截去8个三棱锥后，剩下的凸多面体体积为(D)A.B.C.D.解析：每个截去的小三棱锥体积为×(××)×＝×()4，则剩余部分的体积为V＝1－×()4×8＝1－＝.6.如图，在△ABC中，AB＝2，BC＝1.5，∠ABC＝120°，若使△ABC绕直线BC旋转一周，则所形成的几何体的体积是(D)A.πB.πC.πD.π解析：如图，作AD⊥BC，垂足为D，则在Rt△ABD中，DB＝1，AD＝.∴所求几何体的体积为π·AD2·CD－π·AD2·BD＝π·AD2·BC＝×π×()2×＝π.故选D.7．正方体的内切球与其外接球的体积之比为(C)A．1B．13C．13D．19解析：设正方体的棱长为1，则正方体内切球的半径为棱长的一半即为，外接球的直径为正方体的体对角线，∴外接球的半径为，∴正方体的内切球与其外接球的体积之比为π×3π×3＝13.8．现有一个封闭的正三棱柱容器，高为3，内装水若干(如图甲，底面处于水平状态)．将容器放倒(如图乙，一个侧面处于水平状态)，这时水面所在的平面EE1F1F与各棱的交点分别为其所在棱的中点，则图甲中水面的高度为(D)A.B．2C.D.解析：设正三棱柱的底面积为S，则VABCA1B1C1＝3S. E，F，F1，E1分别为其所在棱的中点，∴＝，即S△AFE＝S，∴S四边形BCFE＝S， VBCFEB1C1F1E1＝S×3＝S，∴题图甲中水面的高度为.故选D.9．如图，一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径相等，这时圆柱、圆锥、球的体积之比为312.解析：设球的半径为R，则V圆柱＝πR2·2R＝2πR3，V圆锥＝πR2·2R＝πR3，V球＝πR3，故V圆柱V圆锥V球＝2πR3πR3πR3＝312.10．将边长为a的正方形ABCD沿对角线AC折起，使BD＝a，则三棱锥DABC的体积为a3.解析： BA＝BC＝BD，∴B点在面ACD上的射影为△ACD的外心，即等腰直角△ADC斜边中点O，OD＝a，∴OB＝a，∴V三棱锥DABC＝×a×a2＝a3.11．一个球内切于底面半径为，高为3的圆锥内，则内切球半径是1；内切球与该圆锥的体积之比为.解析：设球的半径为r，则对圆锥轴截面运用等面积法可得×2×3＝(2＋2×2)r，∴r＝1，内切球与该圆锥的体积之比为＝.三、解答题写出必要的计算步骤，只写最后结果不得分，12、13、15题各12分，14题6分，共42分12．某组合体的直观图如图所示，它的中间为圆柱形，左右两端均为半球形，如图中r＝1，l＝3，试求该组合体的表面积和体积．解：该组合体的表面积S＝4πr2＋2πrl＝4π×12＋2π×1×3＝10π.该组合体的体积V＝πr3＋πr2l＝π×13＋π×12×3＝.13．如图所示，正方体ABCDA1B1C1D1的棱长为a，过顶点B，D，A1截下一个三棱锥．(1)求剩余部分的体积；(2)求三棱锥AA1BD的体积及高．——素养提升——14．表面积为的正四面体的各个顶点都在同一个球面上，则此球的体积为(A)A.πB.πC.πD.π解析：如图所示，将正四面体补形成一个正方体．设正四面体的棱长为a. 正四面体的表面积为，∴4×a2＝，解得a＝，∴正方体的棱长是，又 球的直径是正方体的体对角线，设球的半径是R，∴2R＝×，∴R＝，∴球...