高中数学 1.1正弦定理（一）课时作业 苏教版必修5VIP专享VIP免费

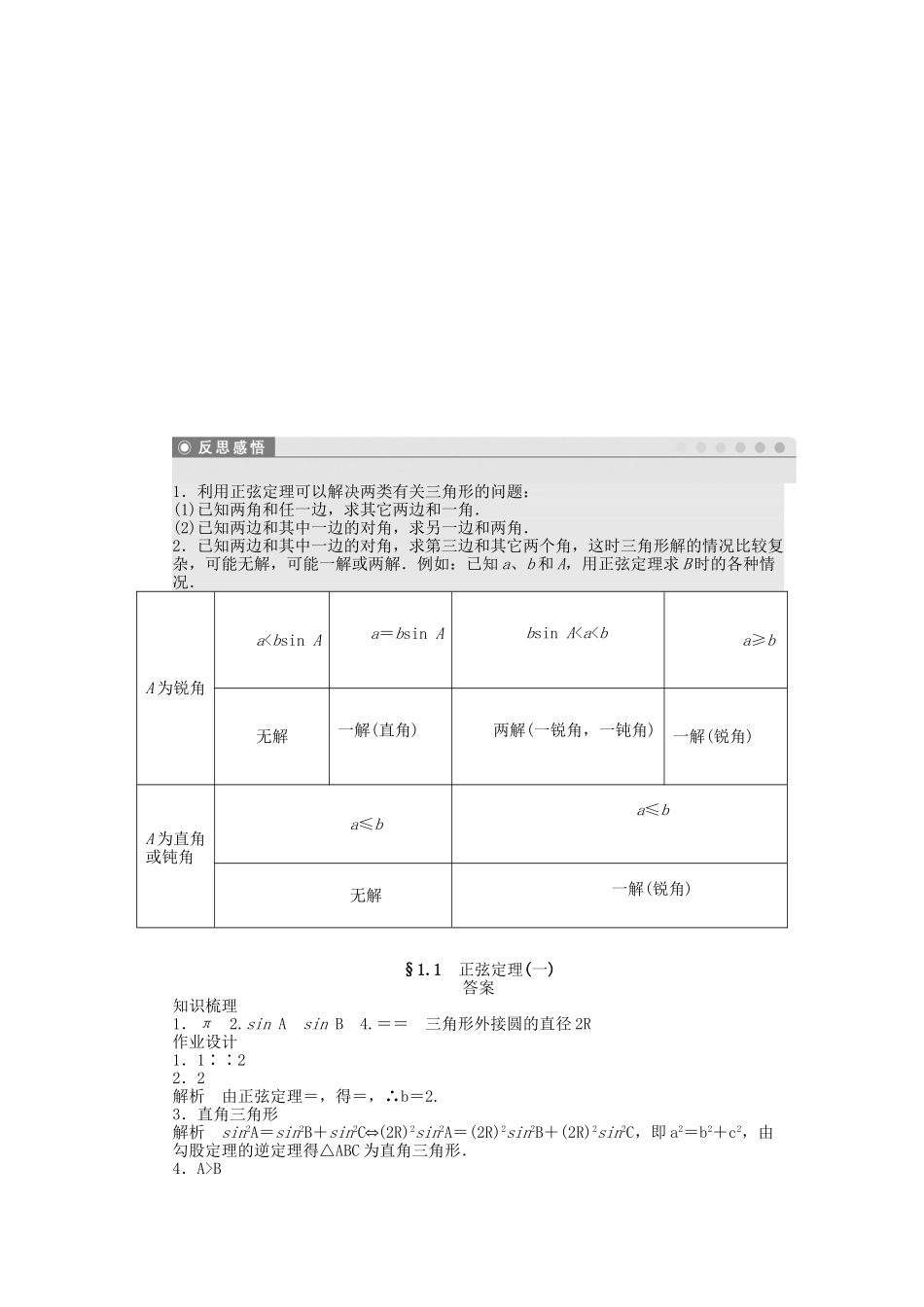
1.1正弦定理(一)课时目标1.熟记正弦定理的内容；2.能够初步运用正弦定理解斜三角形．1．在△ABC中，A＋B＋C＝______，＋＋＝.2．在Rt△ABC中，C＝，则＝________，＝_______________________________.3．一般地，把三角形的三个角A，B，C和它们的对边a，b，c叫做三角形的元素．已知三角形的几个元素求其他元素的过程叫做解三角形．4．正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，即______，这个比值是________________．一、填空题1．在△ABC中，角A，B，C的对边分别是a，b，c，若A∶B∶C＝1∶2∶3，则a∶b∶c等于________．2．若△ABC中，a＝4，A＝45°，B＝60°，则边b的值为____________．3．在△ABC中，sin2A＝sin2B＋sin2C，则△ABC的形状为________________．4．在△ABC中，若sinA>sinB，则角A与角B的大小关系为________．5．在△ABC中，A＝60°，a＝，b＝，则B等于______________．6．在△ABC中，AC＝，BC＝2，B＝60°，则C＝___________________________.7．在△ABC中，若tanA＝，C＝150°，BC＝1，则AB＝________.8．在△ABC中，b＝1，c＝，C＝，则a＝________.9．在△ABC中，已知a，b，c分别为内角A，B，C的对边，若b＝2a，B＝A＋60°，则A＝______.10．在△ABC中，角A，B，C所对的边分别为a，b，c，如果c＝a，B＝30°，那么角C等于________．二、解答题11．在△ABC中，已知a＝2，A＝30°，B＝45°，解三角形．12．在△ABC中，已知a＝2，b＝6，A＝30°，解三角形．能力提升13．在△ABC中，角A，B，C所对的边分别为a，b，c若a＝，b＝2，sinB＋cosB＝，则角A的大小为________．14．在锐角三角形ABC中，A＝2B，a，b，c所对的角分别为A，B，C，求的取值范围．1．利用正弦定理可以解决两类有关三角形的问题：(1)已知两角和任一边，求其它两边和一角．(2)已知两边和其中一边的对角，求另一边和两角．2．已知两边和其中一边的对角，求第三边和其它两个角，这时三角形解的情况比较复杂，可能无解，可能一解或两解．例如：已知a、b和A，用正弦定理求B时的各种情况．A为锐角aB解析由sinA>sinB⇔2RsinA>2RsinB⇔a>b⇔A>B.5．45°解析由＝得sinB＝＝＝.∵a>b，∴A>B，B<60°∴B＝45°.6．75°解析由正弦定理得＝，∴sinA＝.∵BC＝2bsinA，所以本题有两解，由正弦定理得：sinB＝＝＝，故B＝60°或120°.当B＝60°时，C＝90°，c＝＝4；当B＝120°时，C＝30°，c＝a＝2.所以B＝60°，C＝90°，c＝4或B＝120°，C＝30°，c＝2.13.解析∵sinB＋cosB＝sin(＋B)＝.∴sin(＋B)＝1.又0