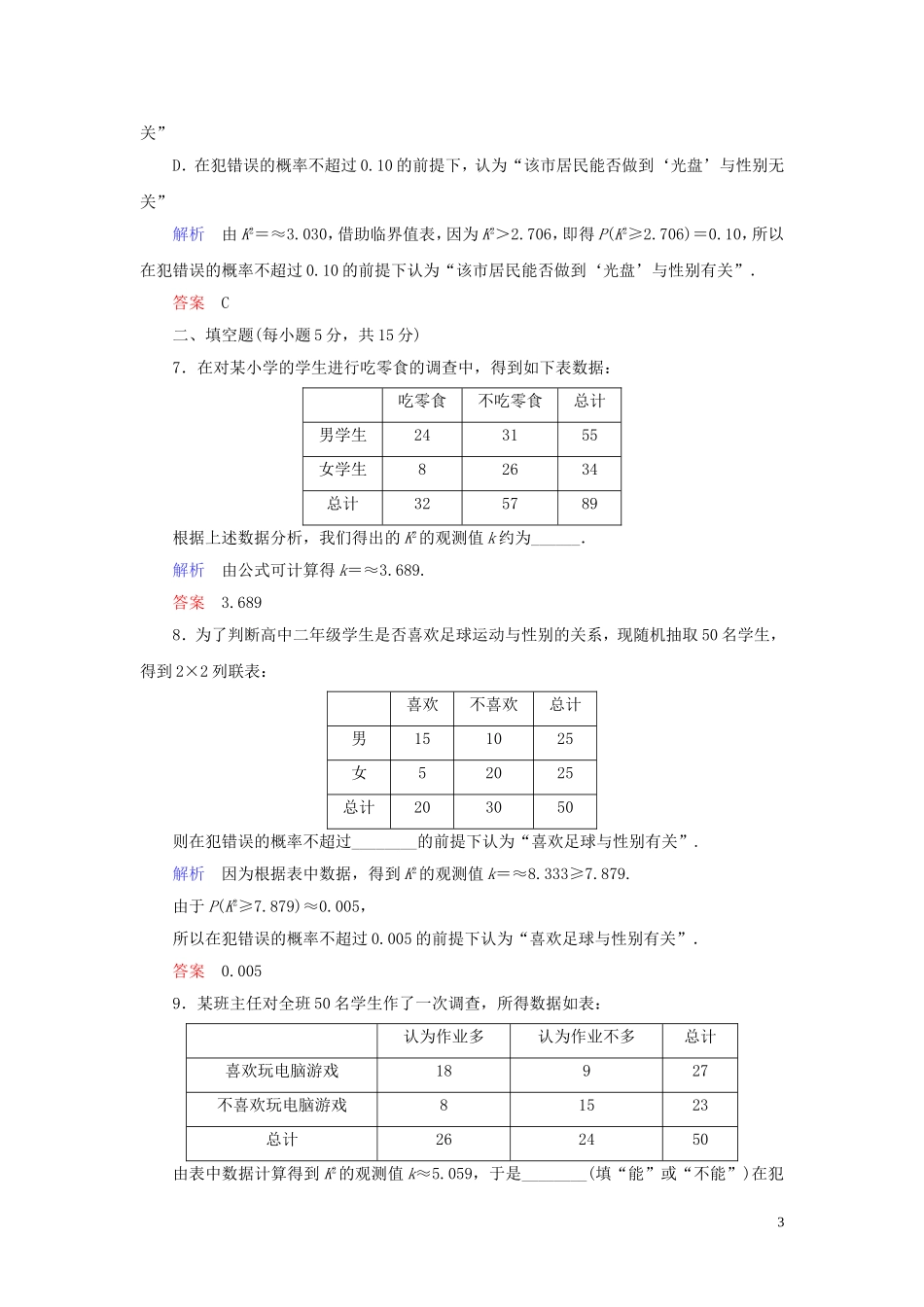
1-2独立性检验的基本思想及其初步应用[课后提升案·素养达成][限时45分钟;满分80分]一、选择题(每小题5分,共30分)1.在一项学生近视情况的调查中,某校男生150名中有80名近视,女生140名中有70名近视,在检验这些中学生眼睛近视是否与性别有关时用什么方法最有说服力A.平均数与方差B.回归分析C.独立性检验D.概率解析判断两个分类变量是否有关的最有效方法是进行独立性检验.答案C2.给出下列实际问题:①一种药物对某种病的治愈率;②两种药物治疗同一种病是否有区别;③吸烟者得肺病的概率;④吸烟是否与性别有关系;⑤网吧与青少年的犯罪是否有关系.其中用独立性检验可以解决的问题有A.①②③B.②④⑤C.②③④⑤D.①②③④⑤解析独立性检验是判断两个分类变量是否有关系的方法,而①③都是概率问题,不能用独立性检验解决.答案B3.利用独立性检验来考虑两个分类变量X和Y是否有关系时,通过查阅临界值表来确定推断“X与Y有关系”的可信度,如果k>5.024,那么就推断“X和Y有关系”,这种推断犯错误的概率不超过A.0.25B.0.75C.0.025D.0.975解析因为P(k>5.024)=0.025,故在犯错误的概率不超过0.025的条件下,认为“X和Y有关系”.答案C4.下面是调查某地区男女中学生喜欢理科的等高条形图,阴影部分表示喜欢理科的百分比,从图中可以看出1A.性别与喜欢理科无关B.女生中喜欢理科的百分比为80%C.男生比女生喜欢理科的可能性大些D.男生不喜欢理科的百分比为60%解析本题考查学生的识图能力,从图中可以分析,男生喜欢理科的可能性比女生大一些.答案C5.某医疗机构通过抽样调查(样本容量n=1000),利用2×2列联表和卡方统计量,研究患肺病是否与吸烟有关.计算得K2≈4.453,经查临界值表知P(K2≥3.841)≈0.05,则下列结论正确的是A.在100个吸烟的人中约有95个人患肺病B.若某人吸烟,那么他有95%的可能性患肺病C.在犯错误的概率不超过0.05的前提下,认为“患肺病与吸烟有关”D.在犯错误的概率不超过0.95的前提下,认为“患肺病与吸烟有关”解析由独立性假设检验知C正确.答案C6.春节期间,“厉行节约,反对浪费”之风悄悄吹开,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:做不到“光盘”能做到“光盘”男4510女3015附:K2=,则得到的正确结论是A.在犯错误的概率不超过0.010的前提下,认为“该市居民能否做到‘光盘’与性别有关”B.在犯错误的概率不超过0.010的前提下,认为“该市居民能否做到‘光盘’与性别无关”C.在犯错误的概率不超过0.10的前提下,认为“该市居民能否做到‘光盘’与性别有2关”D.在犯错误的概率不超过0.10的前提下,认为“该市居民能否做到‘光盘’与性别无关”解析由K2=≈3.030,借助临界值表,因为K2>2.706,即得P(K2≥2.706)=0.10,所以在犯错误的概率不超过0.10的前提下认为“该市居民能否做到‘光盘’与性别有关”.答案C二、填空题(每小题5分,共15分)7.在对某小学的学生进行吃零食的调查中,得到如下表数据:吃零食不吃零食总计男学生243155女学生82634总计325789根据上述数据分析,我们得出的K2的观测值k约为______.解析由公式可计算得k=≈3.689.答案3.6898.为了判断高中二年级学生是否喜欢足球运动与性别的关系,现随机抽取50名学生,得到2×2列联表:喜欢不喜欢总计男151025女52025总计203050则在犯错误的概率不超过________的前提下认为“喜欢足球与性别有关”.解析因为根据表中数据,得到K2的观测值k=≈8.333≥7.879.由于P(K2≥7.879)≈0.005,所以在犯错误的概率不超过0.005的前提下认为“喜欢足球与性别有关”.答案0.0059.某班主任对全班50名学生作了一次调查,所得数据如表:认为作业多认为作业不多总计喜欢玩电脑游戏18927不喜欢玩电脑游戏81523总计262450由表中数据计算得到K2的观测值k≈5.059,于是________(填“能”或“不能”)在犯3错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关.解析查表知若要在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关,则临界值k0=6.635.本题中,k≈5.059<6.635,所以不能在犯错误的概率不...