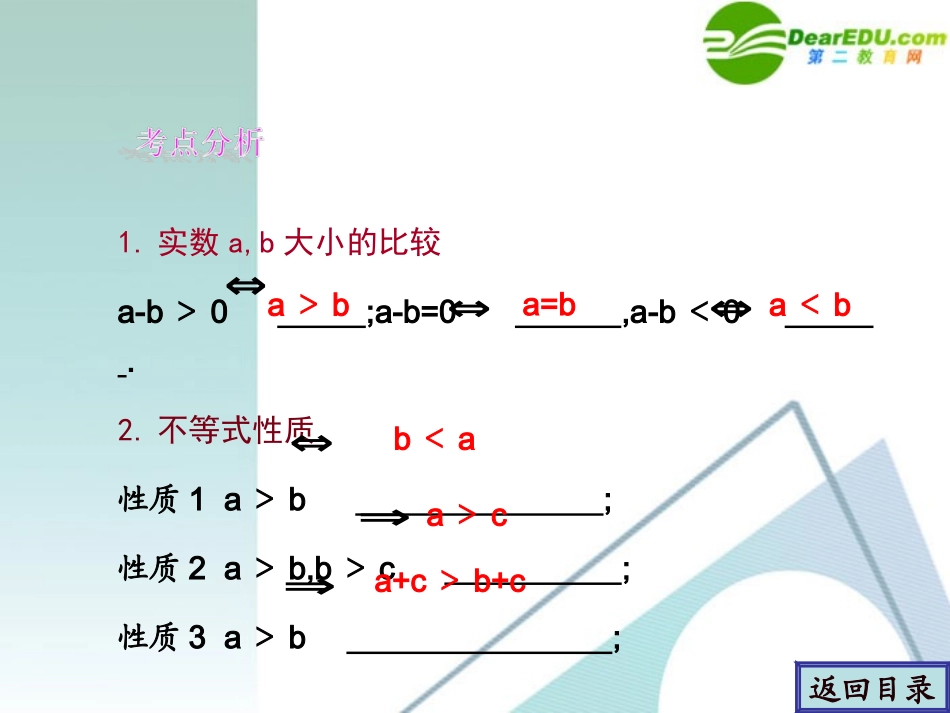
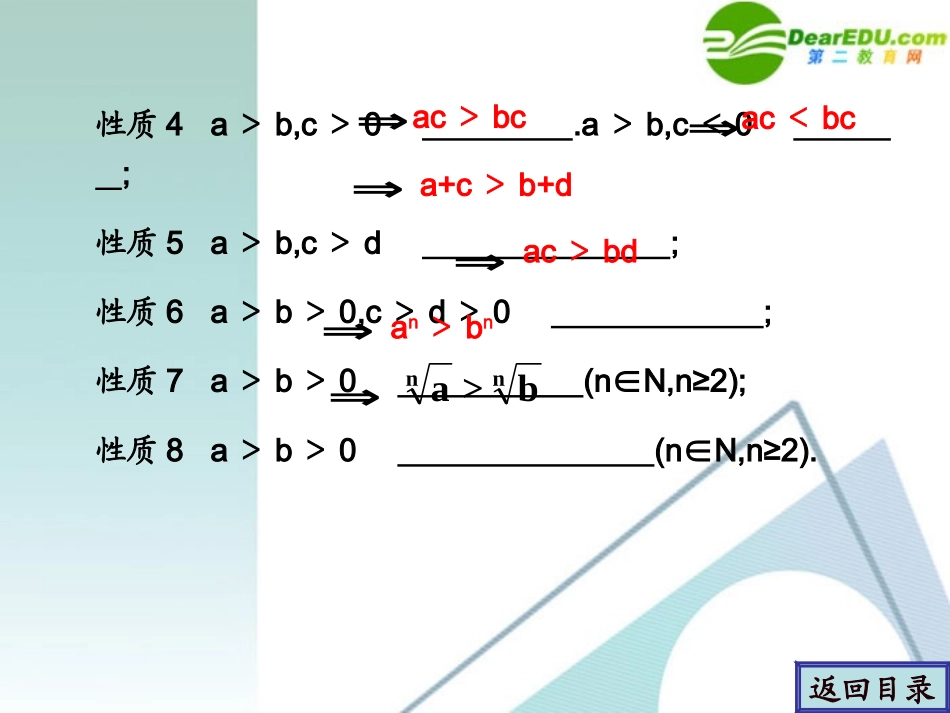
学案学案11不等关系与不等式不等关系与不等式返回目录1.实数a,b大小的比较a-b>0;a-b=0,a-b<0.2.不等式性质性质1a>b;性质2a>b,b>c;性质3a>b;⇔⇔⇔a>ba=ba<b⇔b<aa>ca+c>b+c⇒⇒返回目录性质4a>b,c>0.a>b,c<0;性质5a>b,c>d;性质6a>b>0,c>d>0;性质7a>b>0(nN,n≥2);∈性质8a>b>0(nN,n≥2).∈⇒⇒⇒⇒⇒⇒ac>bcac<bca+c>b+dac>bdan>bnnnb>a返回目录考点一不等式的概念与性质考点一不等式的概念与性质若a>0>b>-a,c<d<0,则下列命题成立的有()①ad>bc;;②③a-c>b-d;a(d-c)④>b(d-c).A.1个B.2个C.3个D.4个0
balgb1ca返回目录CC(命题①不符合不等式的传递性,为假命题.若a>0>b,则,无意义,命题②为假.a>b,c>d中a,b,c,d的符号不确定.若a>0>b,0>c>d,则ac<bd,命题③为假.若a>b>0,ab>0,则,所以,命题④为真.当且cd<0时,ad<bc,所以命题⑤为假.若c>d,则-d>-c,又a>b,所以a+(-d)>b+(-c),即a-d>b-c,命题⑥为真.所以正确的命题只有④⑥.故应选C.)返回目录0>balgb1ab1×adb>ca返回目录【分析】【分析】比较两数(或两式)的大小,一般用比较法,具体用作差比较还是用作商比较应由数(或式)特点而定.考点二大小比较考点二大小比较(1)设x0,b>0,且a≠b,试比较aabb与的大小.2b+a(ab)【解析】【解析】(1)x <y<0,x-y∴<0,x2>y2>0,x+y<0,(x∴2+y2)(x-y)<0,(x2-y2)(x+y)<0,∴(x2+y2)(x-y)>(x2-y2)(x+y).(2)若a>b>0,则>1,a-b>0.由指数函数的性质>1.若b>a>0,则0<<1,a-b<0.由指数函数的性质>1.∴,.∴返回目录1.(ab)ba2b+aba2b+aba(ab)>ba返回目录【评析】【评析】(1)比较两个代数式的大小,可以根据它们的差的符号进行判断,一方面注意题目本身提供的字母的取值范围,另一方面通常将两代数式的差进行因式分解转化为多个因式相乘,或通过配方转化为几个非负实数之和,然后判断正负.(2)作商比较通常适用于两代数式同号的情形.返回目录*对应演练**对应演练*令f(x)=(x-x1)(x-x2),又f(x)=x2+(b-1)x+c,∴x2+bx+c=(x-x1)(x-x2)+x.则t2+bt+c-x1=(t-x1)(t-x2)+t-x1=(t-x1)(t-x2+1).函数f(x)=x2+(b-1)x+c的图象与x轴交于(x1,0),(x2,0),且x2-x1>1.当t<x1时,比较t2+bt+c与x1的大小. t<x1,t-x∴1<0.又x2-x1>1,-x∴2<-x1-1,∴t-x2+1<-x1-1+t+1,即t-x2+1<t-x1<0.∴(t-x1)(t-x2+1)>0,∴t2+bt+c>x1.返回目录返回目录【分析】【分析】将2a+3b用a+b和a-b表示出来,再利用不等式的性质求解2a+3b的范围.考点三范围问题考点三范围问题已知-1<a+b<3且2<a-b<4,求2a+3b的取值范围.【解析】【解析】设2a+3b=m(a+b)+n(a-b),m+n=2m-n=3,∴m=,n=-.∴2a+3b=(a+b)-(a-b). -1<a+b<3,2<a-b<4,∴-<,-2<(a-b)<-1,∴-<(a+b)-(a-b)<,即-<2a+3b<.返回目录∴{252525215