高中数学312瞬时速度与瞬时加速度 试题VIP免费

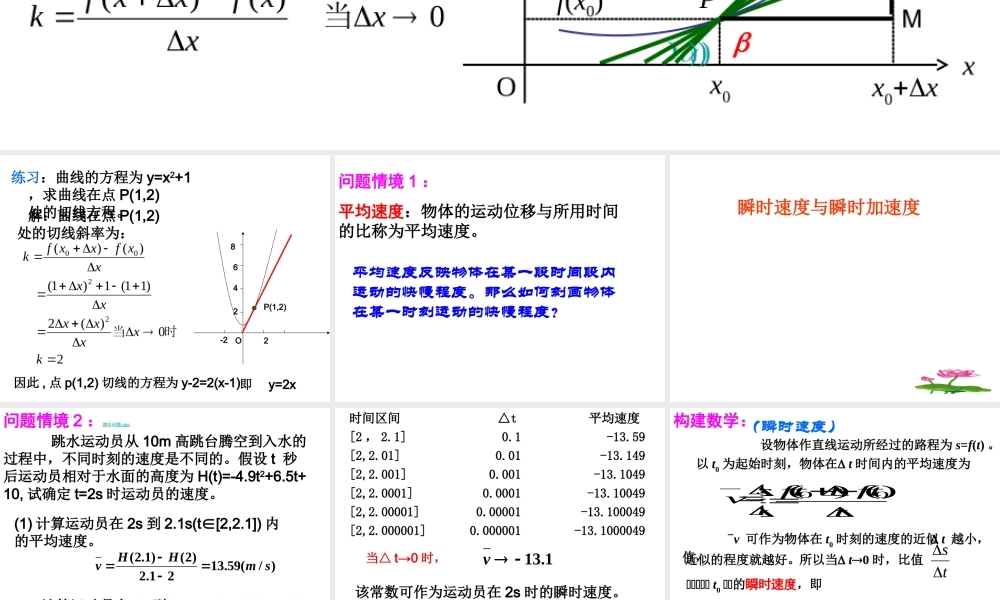
T T f(x0x)x0xQx0Py=f(x)Ox y f(x0)β))Q)QM 当x0 时，动点 Q 将沿曲线趋近于定点 P ，从而割线 PQ也将随之变动而趋向于切线 PT 。此时割线 PQ 的斜率趋向于切线 PT 的斜率 , 当△ x→0 时，割线 PQ 的斜率的逼近值，就是曲线在点 P 处的切线的斜率，即0)()(xxxfxxfk当1. 曲线上一点处的切线斜率： 设曲线 C 是函数 y=f(x) 的图象 , 在曲线 C 上取一点 P(x,y) 及邻近的一点 Q(x +x, f(x+ x)) ，过 P 、 Q 两点作割线， , 则割线 PQ 的斜率为 tg 0limxtg 0limx xy0limxx xfxxf)()(00。PQk复习回顾： 练习：曲线的方程为 y=x2+1 ，求曲线在点 P(1,2)处的切线方程。20)(2)11(1)1()()(2200kxxxxxxxxfxxfk时当O2-22468．因此 , 点 p(1,2) 切线的方程为 y-2=2(x-1)即 y=2xP(1,2) 解：曲线在点 P(1,2)处的切线斜率为： 平均速度：物体的运动位移与所用时间的比称为平均速度。平均速度反映物体在某一段时间段内运动的快慢程度。那么如何刻画物体在某一时刻运动的快慢程度？问题情境 1 ： 瞬时速度与瞬时加速度 问题情境 2 ：跳水问题.gsp 跳水运动员从 10m 高跳台腾空到入水的过程中，不同时刻的速度是不同的。假设 t 秒后运动员相对于水面的高度为 H(t)=-4.9t2+6.5t+10, 试确定 t=2s 时运动员的速度。(1) 计算运动员在 2s 到 2.1s(t[2,2.1])∈内的平均速度。)/(59.1321.2)2()1.2(smHHv(2) 计算运动员在 2s 到 2+⊿t s(t[2,2+∈⊿t])内的平均速度。 时间区间 △t 平均速度[2 ， 2.1]0.1-13.59[2,2.01]0.01-13.149[2,2.001]0.001-13.1049[2,2.0001]0.0001-13.10049[2,2.00001]0.00001-13.100049[2,2.000001]0.000001-13.1000049当△ t→0 时，1.13v该常数可作为运动员在 2s 时的瞬时速度。 设物体作直线运动所经过的路程为 s=f(t) 。 以 t0 为起始时刻，物体在 t 时间内的平均速度为 vt tfttfts)()(00。当当当当当 t0 当当的瞬时速度，即 v 可作为物体在 t0 时刻的速度的近似值， t 越小，近似的程度就越好。所以当 t0 时，比值 vt tfttfts)()(00。（瞬时速度）构建数学：ts时当的瞬时速度在0)()(000tttfttftv 例 1 ：设一辆轿车在公路上做加速直线运动，假设 t s 时的速度为 v(t)=t2+3,（ 1 ）求 t=3s 时轿车的加速度；（ 2 ）求 t=t0s 时轿车的加速度。练习 P62 1 、 2 、3