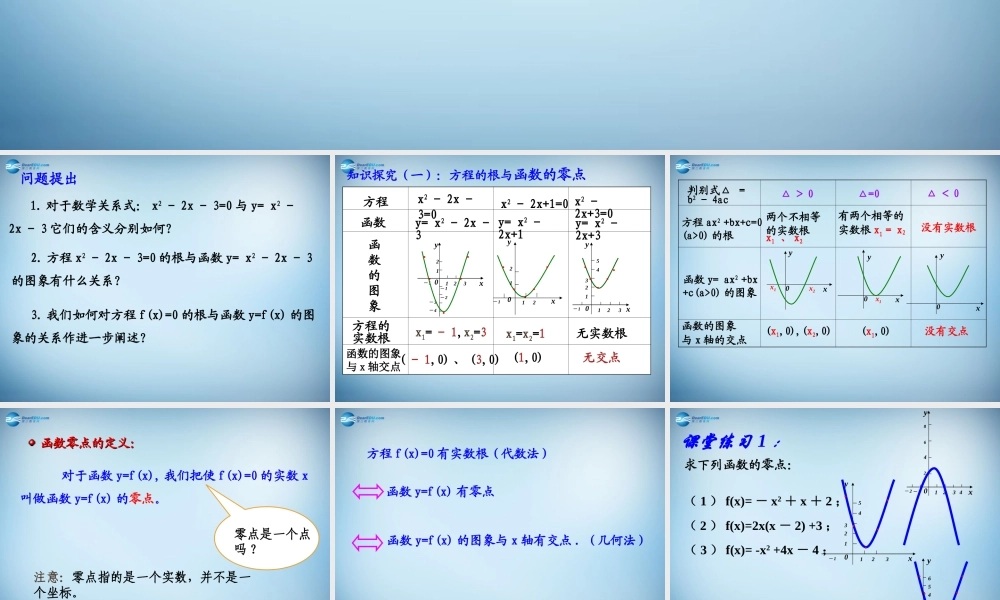
3.1.1 方程的根与函数的零点问题提出 1. 对于数学关系式: x2 - 2x - 3=0 与 y= x2 -2x - 3 它们的含义分别如何? 2. 方程 x2 - 2x - 3=0 的根与函数 y= x2 - 2x - 3的图象有什么关系? 3. 我们如何对方程 f(x)=0 的根与函数 y=f(x) 的图象的关系作进一步阐述? 函数的图象与 x 轴交点方程x2 - 2x+1=0 x2 -2x+3=0y= x2 - 2x -3y= x2 -2x+1函数函数的图象方程的实数根x1= - 1,x2=3x1=x2=1无实数根( - 1,0) 、 (3,0)(1,0)无交点x2 - 2x -3=0xy0- 132112- 1- 2- 3- 4..........xy0- 132112543.. . ..yx0- 12112y= x2 -2x+3知识探究(一):方程的根与函数的零点方程 ax2 +bx+c=0(a>0) 的根函数 y= ax2 +bx+c(a>0) 的图象判别式△ =b2 - 4ac△ > 0△=0△ < 0函数的图象与 x 轴的交点有两个相等的实数根 x1 = x2没有实数根xyx1x20xy0x1xy0(x1,0),(x2,0)(x1,0)没有交点两个不相等的实数根x1 、 x2 对于函数 y=f(x), 我们把使 f(x)=0 的实数 x叫做函数 y=f(x) 的零点。函数零点的定义:函数零点的定义:注意:零点指的是一个实数,并不是一个坐标。零点是一个点吗 ?函数 y=f(x) 有零点方程 f(x)=0 有实数根 ( 代数法 )函数 y=f(x) 的图象与 x 轴有交点 . (几何法)课堂练习 1 :求下列函数的零点:( 1 ) f(x)= - x2 + x + 2 ;( 2 ) f(x)=2x(x - 2) +3 ;( 3 ) f(x)= -x2 +4x - 4 ;xy0- 13214862- 24xy0- 132112543 ..........xy0- 132112543640123 4 5-1-212345-1-2-3-4xy探究 观 察 二 次 函 数2( )23f xxx的 图象,如右图,我们发现函数2( )23f xxx 在区间2,1上有零点。计算( 2)f 和(1)f的乘积,你能发现这个乘积有什么特点?在区间2,4 上是否也具有这种特点呢? 知识探究(二):函数零点存在性原理 结论如果函数( )yf x在区间,a b 上的图象是连续不断的一条曲线, 并且有 ( )( )0f af b ,那么,函数( )yf x在区间,a b 内有零点, 即存在,ca b,使得 ( )0f c ,这个c也就是方程 ( )0f x 的根。 由以上探索,你可以得出什么样的结论?由以上探索,你可以得出什么样的结论?结论理解如果函数( )yf x在区间,a b 上的图象是连续不断的...