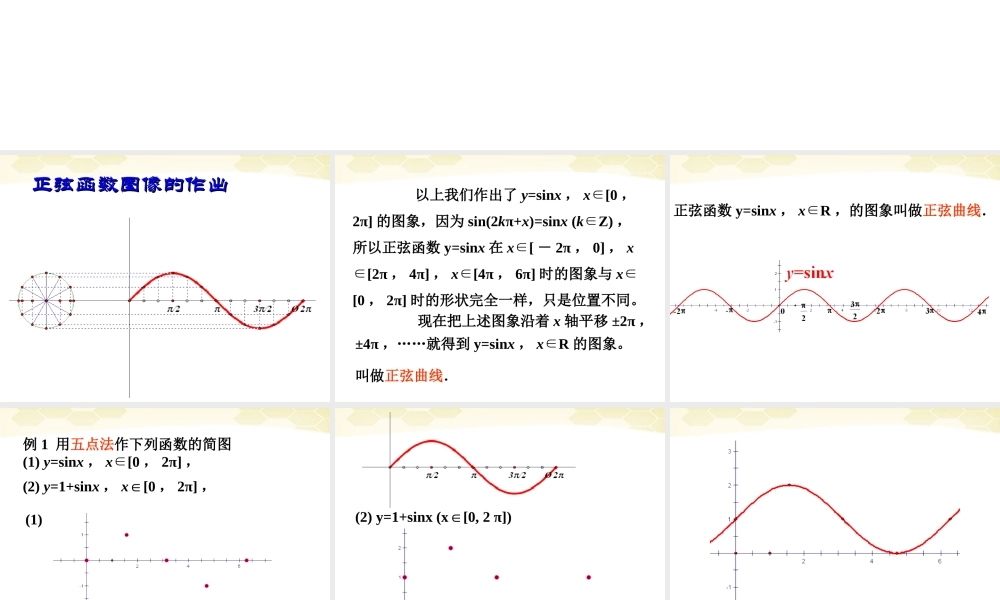
1.3.11.3.1 正弦函数图像与性质正弦函数图像与性质 正弦函数图像的作出正弦函数图像的作出 以上我们作出了 y=sinx , x[0∈,2π] 的图象,因为 sin(2kπ+x)=sinx (k∈Z) ,所以正弦函数 y=sinx 在 x[∈ - 2π , 0] , x[2∈π , 4π] , x[4∈π , 6π] 时的图象与 x∈[0 , 2π] 时的形状完全一样,只是位置不同。 现在把上述图象沿着 x 轴平移 ±2π ,±4π ,……就得到 y=sinx , xR∈的图象。叫做正弦曲线. 正弦函数 y=sinx , xR∈,的图象叫做正弦曲线. 例 1 用五点法作下列函数的简图(1) y=sinx , x[0∈, 2π] , (2) y=1+sinx , x[0∈, 2π] , (1) (2) y=1+sinx (x[0, 2 π])∈ 例 2 利用正弦函数的图象,求满足下列条件的 x 的集合:21sinx解:在 y 轴上取点 (0, 0.5) ,过该点作 x 轴的平行线 , 与正弦函数图象相交于点 等,所以不等式的解集是1(, )6 251(, )625{ | 22,}66xkxkkZ 正弦函数 y=sinx 性质 (1) 定义域:y=sinx 的定义域是实数集 R(2) 值域 : 正弦函数的值域是[- 1 , 1 ] .2① 当且仅当 x = + 2kπ , kZ∈时,正弦函数取得最大值 1 ;2② 当且仅当 x =- + 2kπ , kZ∈时,正弦函数取得最小值- 1 (3) 周期性 : 由 sin(x + 2kπ) = sinx (kZ)∈知: 正弦函数值是按照一定规律不断重复地取得的这种性质称为三角函数的周期性。正弦函数 y=sinx 性质 对于函数 f(x) ,如果存在一个非零常数 T ,使得定义域内任意 x ,都有 f(x + T) = f(x) ,那么函数 f(x) 就叫做周期函数,非零常数T 叫做这个函数的周期。 对于一个周期函数 f(x) ,如果在它所有的周期中存在一个最小的正数,那么这个最小正数就叫做 f(x) 的最小正周期。(有些周期函数没有最小正周期) . 注意:(1) 周期函数中, x 定义域 M ,则必有 x+TM, 且若 T>0 ,则定义域无上界; T<0 则定义域无下界;(2) “ 每一个值”,只要有一个反例,则 f (x) 就不为周期函数(如 f (x0+T)f (x0) );(3) T 往往是多值的(如 y=sinx, T=2k 都是周期 , 最小正周期是 2π. ) (4) 奇偶性 :由 sin( - x) =- sinx, 可知: y = sinx 为奇函数 ,因此正弦曲线关于原点 O 对称 .(5) 单调性闭区间[-...