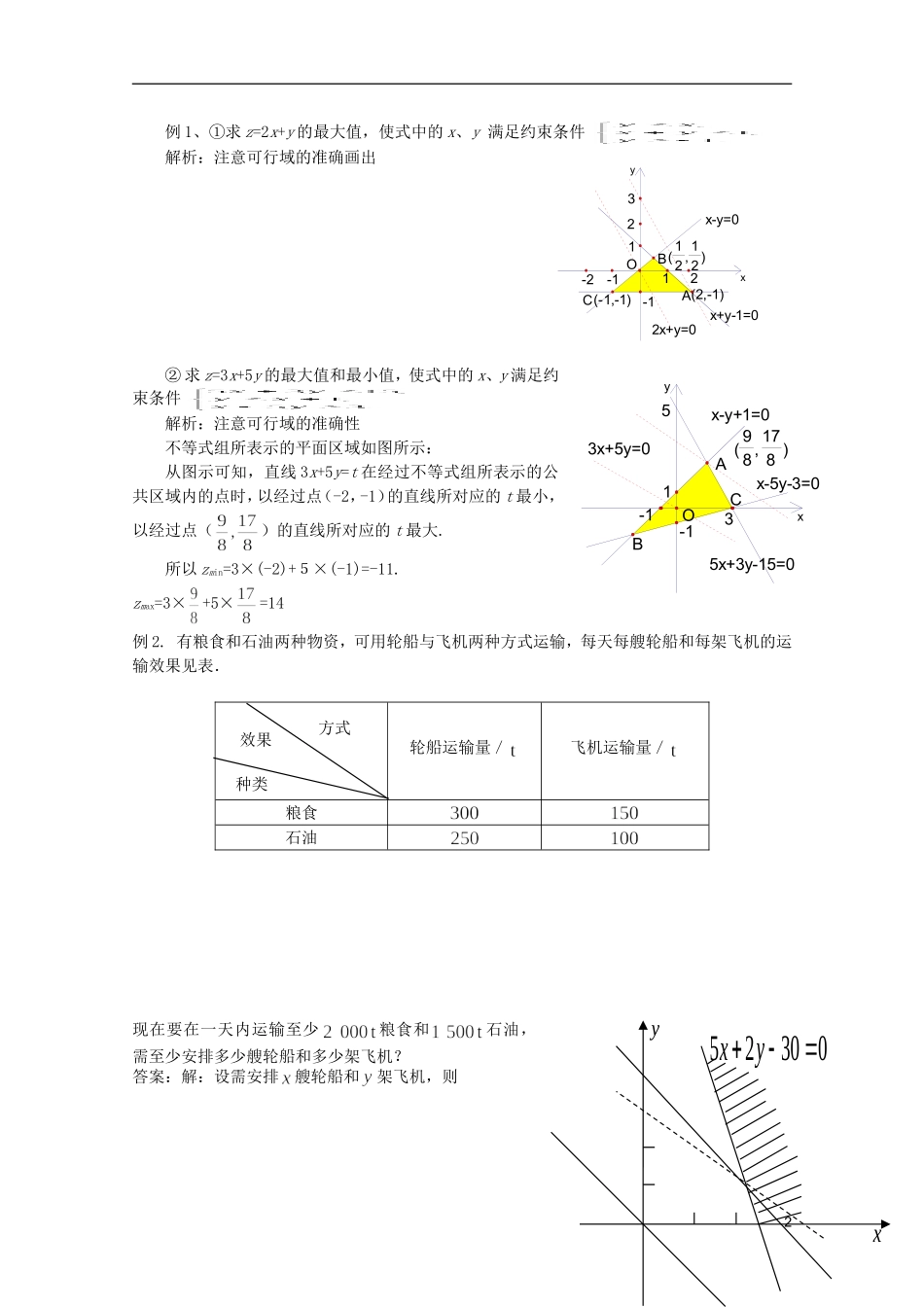
3.3.2 二元一次不等式(组)与平面区域课前预习学案一、预习目标1.了解线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念。2.了解线性规划问题的图解法,并能应用它解决一些简单的实际问题二、预习内容1.阅读课本引例,回答下列问题线性规划的有关概念:① 线性约束条件② 线性目标函数:③ 线性规划问题:一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题.④ 可行解、可行域和最优解:满足线性约束条件的解(x,y)叫可行解.由所有可行解组成的集合叫做可行域.使目标函数取得最大或最小值的可行解叫线性规划问题的最优解2..通过研究引例及例题 5、6,你能总结出求线性规划问题的最值或最优解的步骤吗?那些问题较难解决?课内探究学案一、 学习目标1.了解线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念。2.了解线性规划问题的图解法,并能应用它解决一些简单的实际问题二、学习重难点学习重点:教学重点: 用图解法解决简单的线性规划问题教学难点:准确求得线性规划问题的最优解三、学习过程(一)自主学习大家预习课本 P87 页,并回答以下几个问题:问题 1. ① 线性约束条件② 线性目标函数:③ 线性规划问题:一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题.④ 可行解、可行域和最优解:(二) 合作探究,得出解决线性规划问题的一般步骤(三)典型例题1例 1、①求 z=2x+y 的最大值,使式中的 x、y 满足约束条件解析:注意可行域的准确画出② 求 z=3x+5y 的最大值和最小值,使式中的 x、y 满足约束条件解析:注意可行域的准确性不等式组所表示的平面区域如图所示:从图示可知,直线 3x+5y=t 在经过不等式组所表示的公共区域内的点时,以经过点(-2,-1)的直线所对应的 t 最小,以经过点()的直线所对应的 t 最大.所以 zmin=3×(-2)+5×(-1)=-11.zmax=3×+5×=14例 2. 有粮食和石油两种物资,可用轮船与飞机两种方式运输,每天每艘轮船和每架飞机的运输效果见表.轮船运输量/飞机运输量/粮食石油现在要在一天内运输至少粮食和石油,需至少安排多少艘轮船和多少架飞机?答案:解:设需安排艘轮船和架飞机,则2xy( 12 , 12 )(-1,-1)(2,-1)2x+y=0x+y-1=0x-y=0CBAO21-1-2-1123xy( 98 , 178 )3x+5y=05x+3y-15=0x-y+1=0CBAO3x-5y-3=0-1-115方式效果种类yx5230 0...