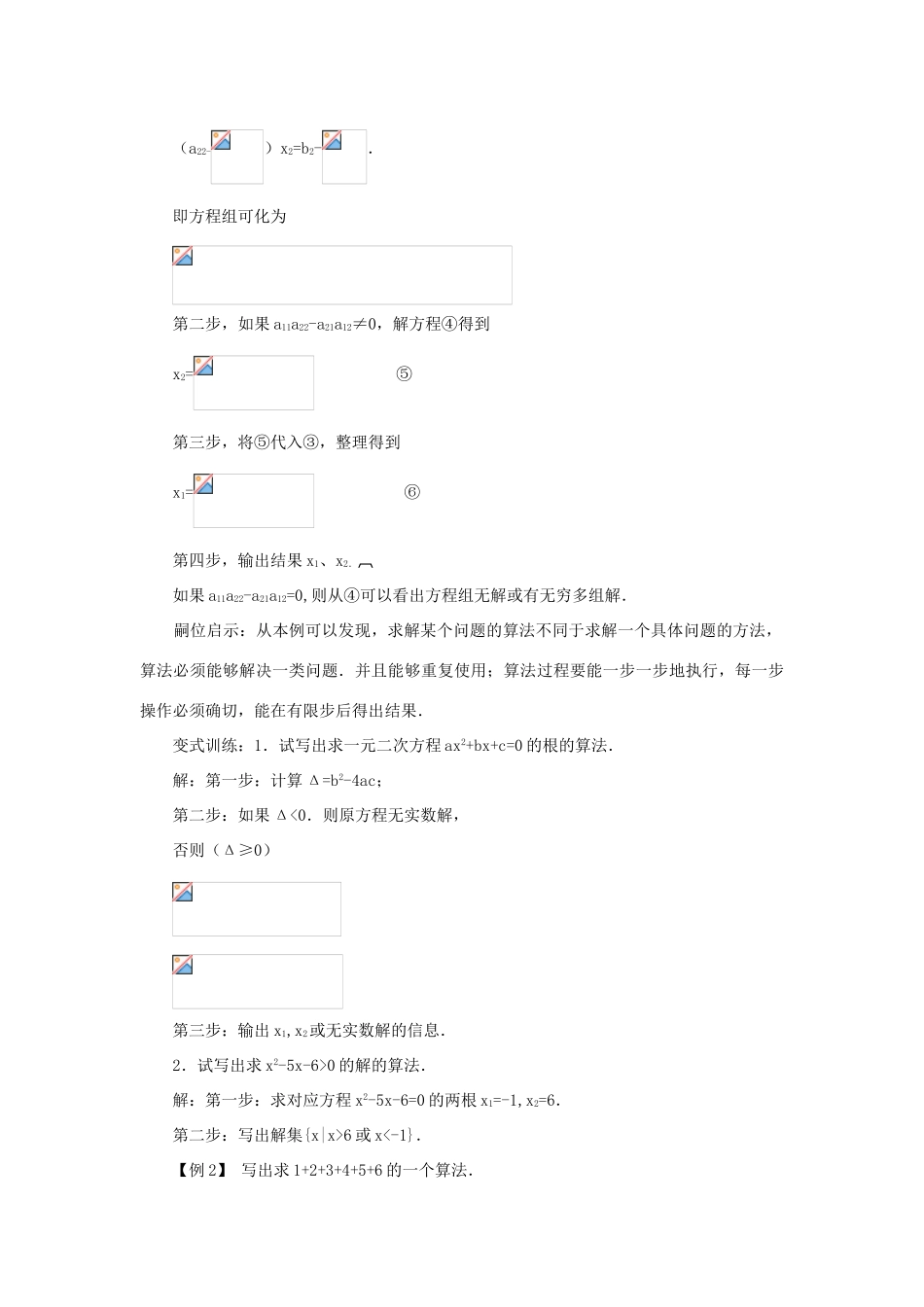
1.1 算法的含义案例探究有 8 个小球,其中 7 个重量相同,仅有一个较重,用天平如何称出那个重的小球. 方法 1:把 8 个小球分成四组,依次将每组放在天平上,直到某一组不平衡,就可确定重的小球,最多需称 4 次. 方法 2:(1)从 8 个小球中任取 6 个小球,将这 6 个小球每边 3 个置于天平上;(2)若天平平衡,则表明重的小球在剩余的 2 个小球中,只需将那两个小球放在天平上再称 1次就可找到重的那个小球;(3)若天平不平衡,则从较重的一边的 3 个球中任取两个球称量,若平衡,则剩下的那个即为要找的小球,若不平衡,则重的那边就是要找的小球. 我们做任何事情,都是在一定条件下按某种顺序执行一系列操作.解决数学问题也常常如此,这就是本节内容要研究的算法思想.自学导引 一般而言,对一类问题机械的、统一的求解方法称为算法.1.算法概念的理解 (1)算法是指可以用计算机来解决的某一类问题的程序或步骤,这些程序或步骤必须是明确有效的,而且能在有限步骤之内完成.(2)算法与一般意义上具体问题的解法既有联系,又有区别,它们之间是特殊与一般的关系,也是抽象与具体的关系.算法的获得要借助一般意义上具体问题的求解方法,而任何一个具体问题都可以利用这类问题的一般算法来解决.(3)算法一方面具有具体化、程序化、机械化的特点,同时又有高度的抽象性、概括性、精确性,所以算法在解决问题中更具条理性、逻辑化特点. 2.算法的五个特点 (1)概括性:写出的算法必须能解决一类问题,并且能重复使用.例如:给出求解方程组的一个算法. 解析:解这个方程组的步骤是: 第一步:②-①×2 得 5y=3; ③ 第二步:解③得 y=; 第三步:将 y=代入①,得 x=. 像上例二元一次方程组的求解问题,也适用于其他二元一次方程组的求解. (2)正确性与顺序性:算法从初始步骤开始,分为若干明确的步骤,前一步是后一步的前提,只有执行完前一步才能进行下一步,而且每一步都是正确无误的,从而组成了一个有着很强逻辑性的序列. (3)有限性:算法有明确的开始和结束界限,终止时表示问题得到解答或指出问题没解,是在有限步骤内求解某一问题. (4)不唯一性:求解某一问题的算法不是唯一的,可以有不同的算法.当然这些算法有繁简之分,但是都能解决这一类问题. (5)普遍性:很多具体的问题,都可以设计合理的算法去解决,例如,手算、心算、用算盘、用计算器算都要经过有...