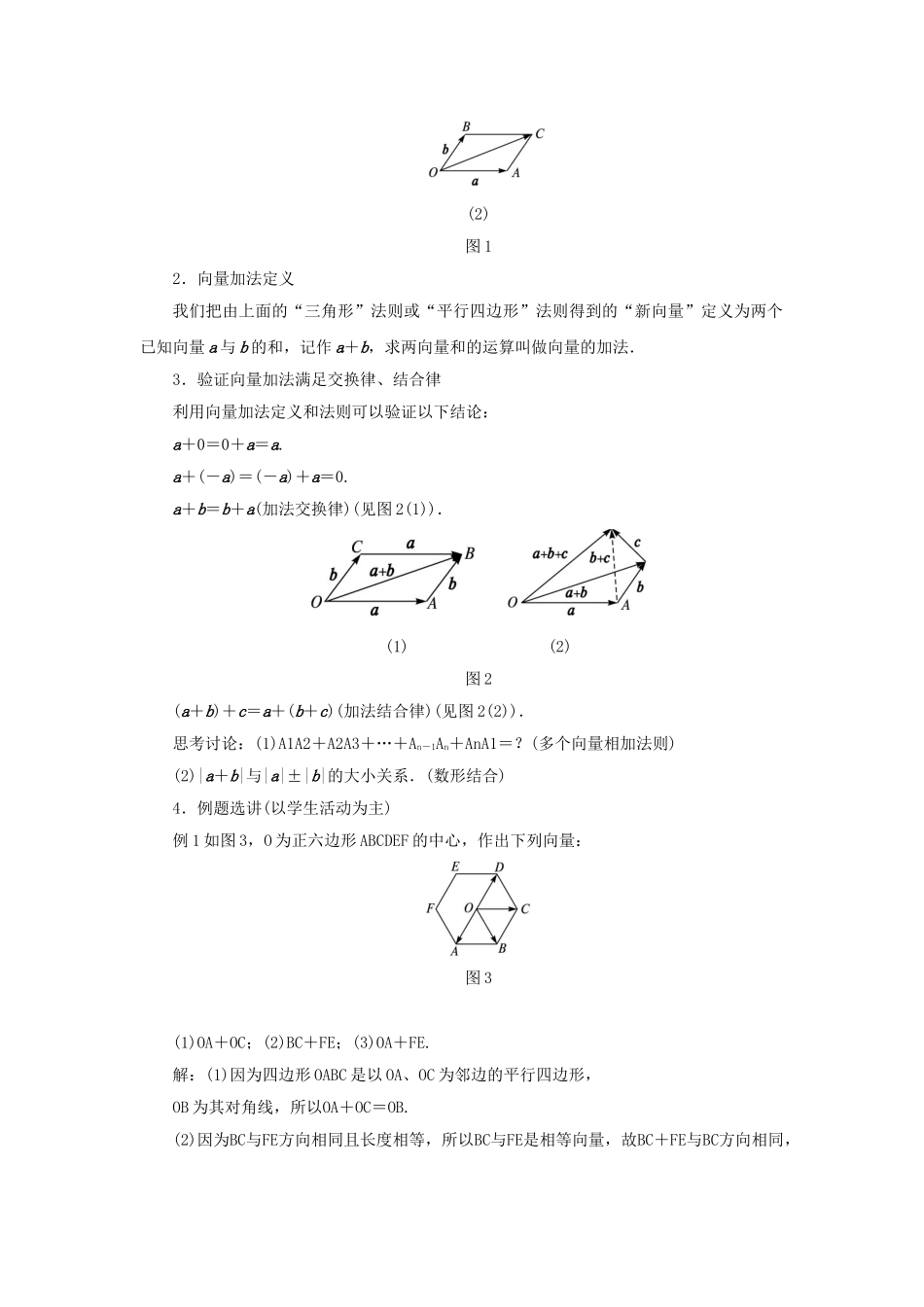
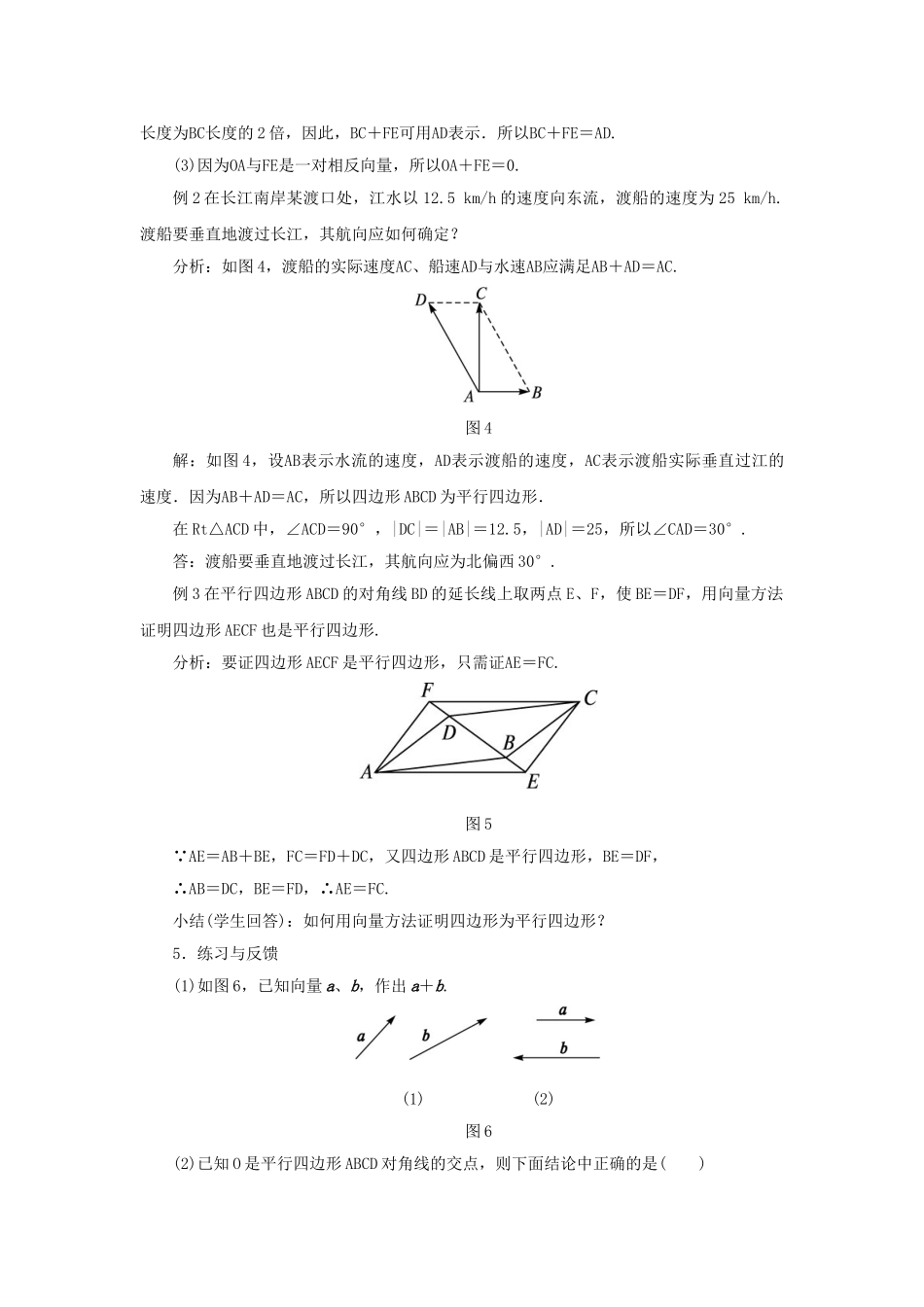
2.2.1 向量的加法作者:陆正海,江苏省泰州中学高级教师、泰州市数学学科带头人,本教学设计获江苏省教学设计大赛三等奖.\s\up7()设计思想 数学定义也是数学思维活动的结果,本节课设计思想是以物理学中“合位移”“合力”等概念为背景,引导学生亲历向量加法的建构过程,使学生体会数学抽象思维活动的基本方法.教学内容分析 本节课教学内容包括向量加法法则的建构,向量加法运算律及运算,以及向量加法的简单应用.教学目标分析 理解向量加法的意义,会用三角形法则和平行四边形法则求作已知两向量的和;掌握向量加法的交换律和结合律,会进行向量加法运算;通过体会、理解向量加法的定义过程对学生进行抽象思维训练,培养学生的创新意识和创造能力.\s\up7()1.情景设置从数学的角度看,向量也是量,数量可以进行运算,向量也必须建立相应的运算系统,才能作为解决实际问题的工具.呈现物理学中“合位移”和“合力”求法,提出问题:已知两个向量,我们是否可以类比“合位移”或“合力”求法,“生成”一个新的向量?探索讨论:已知向量 a 和 b,按照求合位移的方式我们可以这样得到一个新向量:如图,作OA=a,AB=b,连结 OB 得到新向量OB;按照平行四边形求合力的方式我们又可以这样得到一个新向量:如图,作OA=a,OB=b,以 OA、OB 为邻边作平行四边形 OACB,得到新向量OC.当然,利用向量相等概念分析可知,两种方式得到的“新向量”是相等的,这是因为图 1(2)中的AC=OB=b,也就说明由“平行四边形”法则得到的OC(见图 1(2))与由“三角形”法则得到的向量OB(见图 1(1))是相等的. (1) (2)图 12.向量加法定义我们把由上面的“三角形”法则或“平行四边形”法则得到的“新向量”定义为两个已知向量 a 与 b 的和,记作 a+b,求两向量和的运算叫做向量的加法.3.验证向量加法满足交换律、结合律利用向量加法定义和法则可以验证以下结论:a+0=0+a=a.a+(-a)=(-a)+a=0.a+b=b+a(加法交换律)(见图 2(1)). (1) (2)图 2(a+b)+c=a+(b+c)(加法结合律)(见图 2(2)).思考讨论:(1)A1A2+A2A3+…+An-1An+AnA1=?(多个向量相加法则)(2)|a+b|与|a|±|b|的大小关系.(数形结合)4.例题选讲(以学生活动为主)例 1 如图 3,O 为正六边形 ABCDEF 的中心,作出下列向量:图 3(1)OA+OC;(2)BC+FE;(3)OA+FE.解:(1)因为四边形 OABC 是以 OA、OC 为邻边的平行四边形,OB 为其对角线,所...