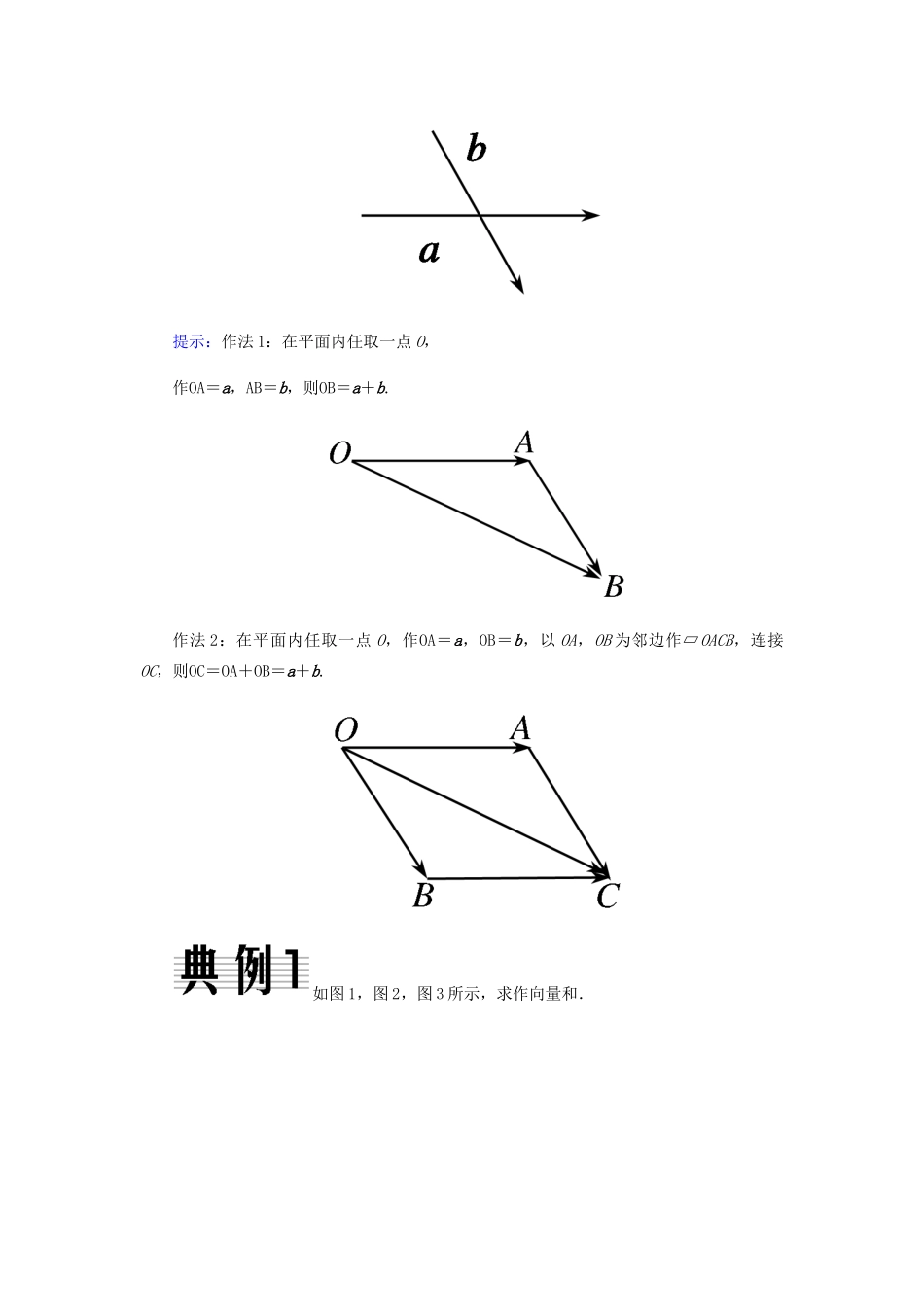
2.2.1 向量加法运算及其几何意义[教材研读]预习课本 P80~83,思考以下问题1.向量的加法如何定义? 2.在求两向量和的运算时,通常使用哪两个法则? 3.向量加法的运算律有哪两条? [要点梳理]1.向量加法的定义及运算法则2.向量加法的运算律[自我诊断]判断(正确的打“√”,错误的打“×”)1.两个向量相加结果可能是一个数量.( )2.两个向量相加实际上就是两个向量的模相加.( )3.任意两个向量的和向量不可能与这两个向量共线.( )[答案] 1.× 2.× 3.×题型一 向量加法及其几何意义思考:如图,已知向量 a,b,分别利用三角形法则和平行四边形法则作出向量 a+b.提示:作法 1:在平面内任取一点 O,作OA=a,AB=b,则OB=a+b.作法 2:在平面内任取一点 O,作OA=a,OB=b,以 OA,OB 为邻边作▱OACB,连接OC,则OC=OA+OB=a+b.如图 1,图 2,图 3 所示,求作向量和.[思路导引] 作向量和时既可用三角形法则也可用平行四边形法则,注意三角形法则是首尾相接,而平行四边形法则需有相同的始点.[解] 如图中①,②所示,首先作OA=a,然后作 AB=b,则OB=a+b.如图③所示,作AB=a,BC=b,则AC=a+b,再作CD=c,则AD=AC+CD=(a+b)+c,即AD=a+b+c. 应用三角形法则和平行四边形法则应注意的问题(1)三角形法则可以推广到 n 个向量求和,作图时要求“首尾相连”,即 n 个首尾相连的向量的和对应的向量是第一个向量的起点指向第 n 个向量的终点的向量.(2)平行四边形法则只适用于不共线的向量求和,作图时要求两个向量的起点重合.(3)求作三个或三个以上的向量和时,用三角形法则更简单.【温馨提示】 向量加法的平行四边形法则和三角形法则的区别和联系.(1)区别:①三角形法则中强调“首尾相接”,平行四边形法则中强调的是“共起点”;②三角形法则适用于任意两个非零向量求和,而平行四边形仅适用于不共线的两个向量求和.(2)联系:①当两个向量不共线时,向量加法的三角形法则和平行四边形法则是统一的;②三角形法则作出的图形是平行四边形法则作出的图形的一半.[跟踪训练]如图,已知 a、b、c,求作向量 a+b+c.[解] 在平面内任取一点 O,如图所示.作OA=a,AB=b,BC=c,则OC=a+b+c.思考:式子AB+BA=0 正确吗?提示:AB+BA的和为零向量,即AB+BA=0,0 不能写成 0,故式子AB+BA=0 不正确.化简下列各式:(1)AB+DF+CD+BC+FA;(2)(AB+DE)+CD+BC+EA.[思路导引...