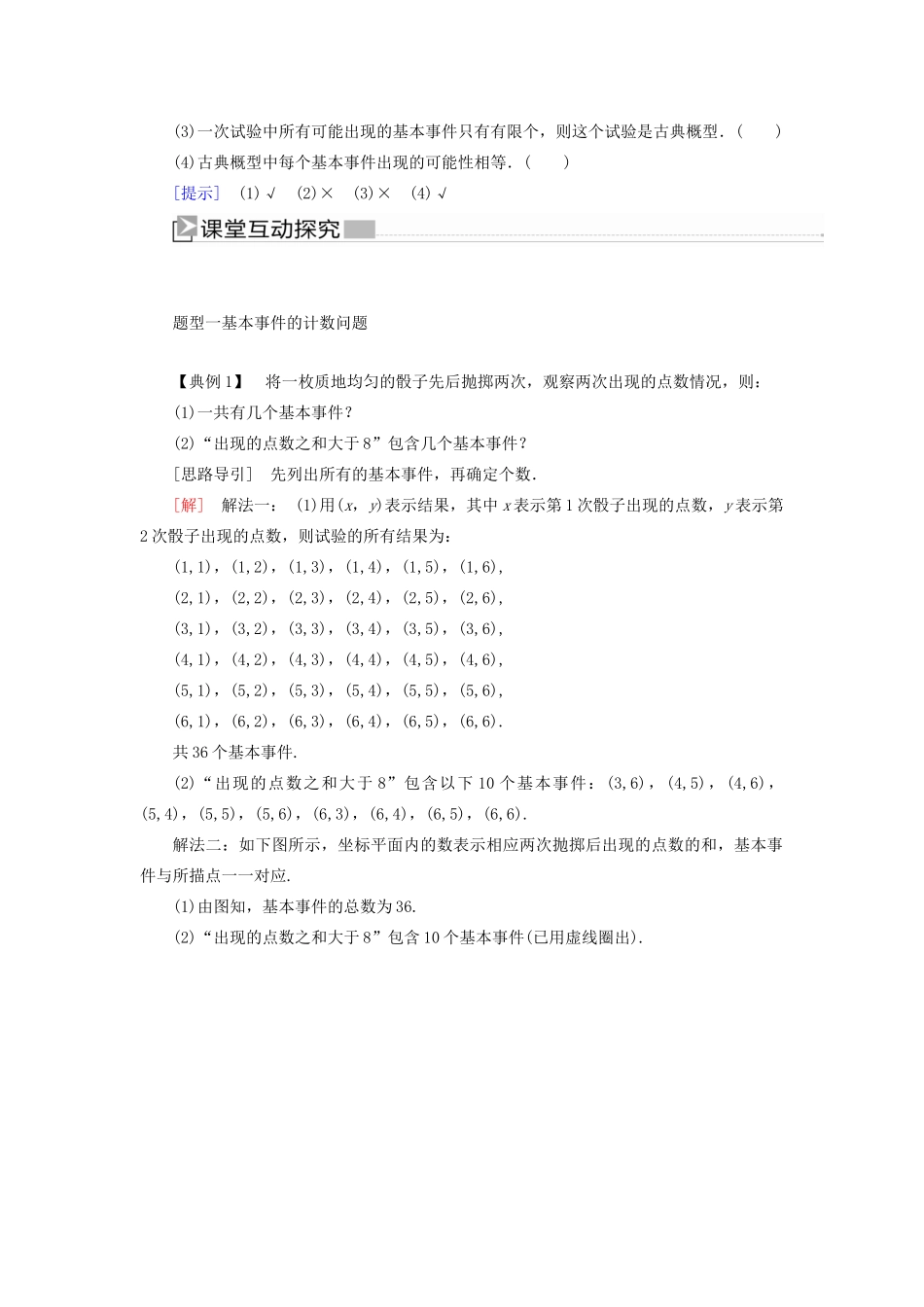
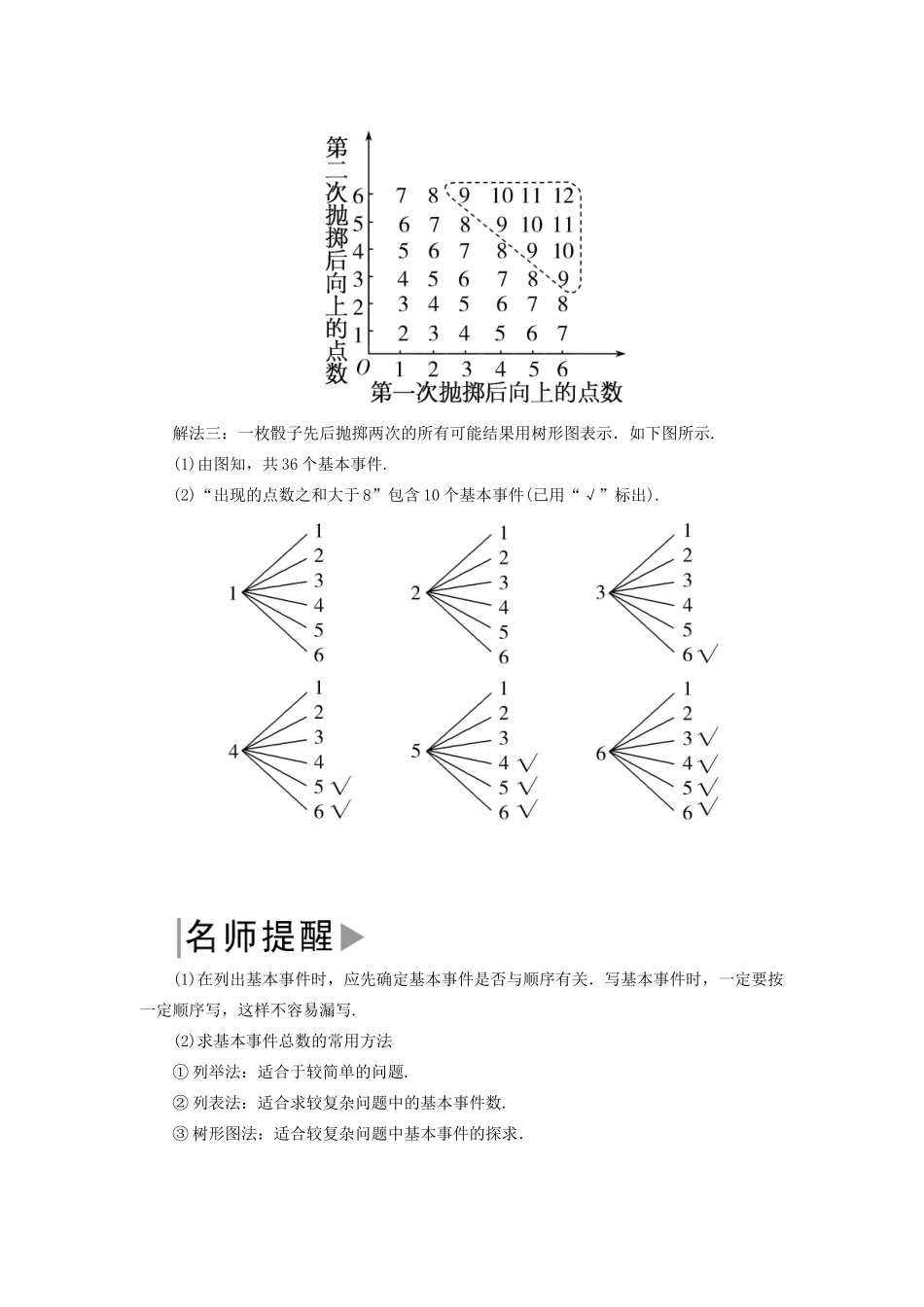
3.2.1 古典概型1.了解基本事件的定义,能写出一次试验所出现的基本事件.2.理解古典概型的特征和计算公式,会判断古典概型,培养逻辑推理的核心素养.3.会求古典概型中事件的概率,培养数学建模的核心素养.1.基本事件(1)定义:在一次试验中,所有可能出现的基本结果中不能再分的最简单的随机事件称为该次试验的基本事件.(2)特点:一是任何两个基本事件是互斥的;二是任何事件(除不可能事件)都可以表示成基本事件的和.2.古典概型(1)定义:如果一个概率模型满足① 试验中所有可能出现的基本事件只有有限个;② 每个基本事件出现的可能性相等.那么这样的概率模型称为古典概率模型,简称古典概型.(2)计算公式:对于古典概型,任何事件的概率为 P(A)=.1.掷一枚不均匀的骰子,求出现点数为偶数点的概率,这个概率模型还是古典概型吗?[提示] 不是.因为骰子不均匀,所以每个基本事件出现的可能性不相等.2.“在区间[0, 10]上任取一个数,这个数恰为 2 的概率是多少?”这个概率模型属于古典概型吗?[提示] 不是.因为在区间[0,10]上任取一个数,其试验结果有无限个,故其基本事件有无限个,所以不是古典概型.3.判断正误.(正确的打“√”,错误的打“×”)(1)任何两个基本事件是互斥的.( )(2)任何事件都可以表示成基本事件的和.( )(3)一次试验中所有可能出现的基本事件只有有限个,则这个试验是古典概型.( )(4)古典概型中每个基本事件出现的可能性相等.( )[提示] (1)√ (2)× (3)× (4)√题型一基本事件的计数问题 【典例 1】 将一枚质地均匀的骰子先后抛掷两次,观察两次出现的点数情况,则:(1)一共有几个基本事件?(2)“出现的点数之和大于 8”包含几个基本事件?[思路导引] 先列出所有的基本事件,再确定个数.[解] 解法一: (1)用(x,y)表示结果,其中 x 表示第 1 次骰子出现的点数,y 表示第2 次骰子出现的点数,则试验的所有结果为:(1,1),(1,2),(1,3),(1,4),(1,5),(1,6), (2,1),(2,2),(2,3),(2,4),(2,5),(2,6), (3,1),(3,2),(3,3),(3,4),(3,5),(3,6), (4,1),(4,2),(4,3),(4,4),(4,5),(4,6), (5,1),(5,2),(5,3),(5,4),(5,5),(5,6), (6,1),(6,2),(6,3),(6,4),(6,5),(6,6). 共 36 个基本事件. (2)“出现的点数之和大于 8”包含以下 10 个基本事件:(3,6),(4,5),(4,6),(5,4),(5,5),(5,6),(6,3),(6,4),(6,5),(6,6). 解法二:如下图所示,坐标...