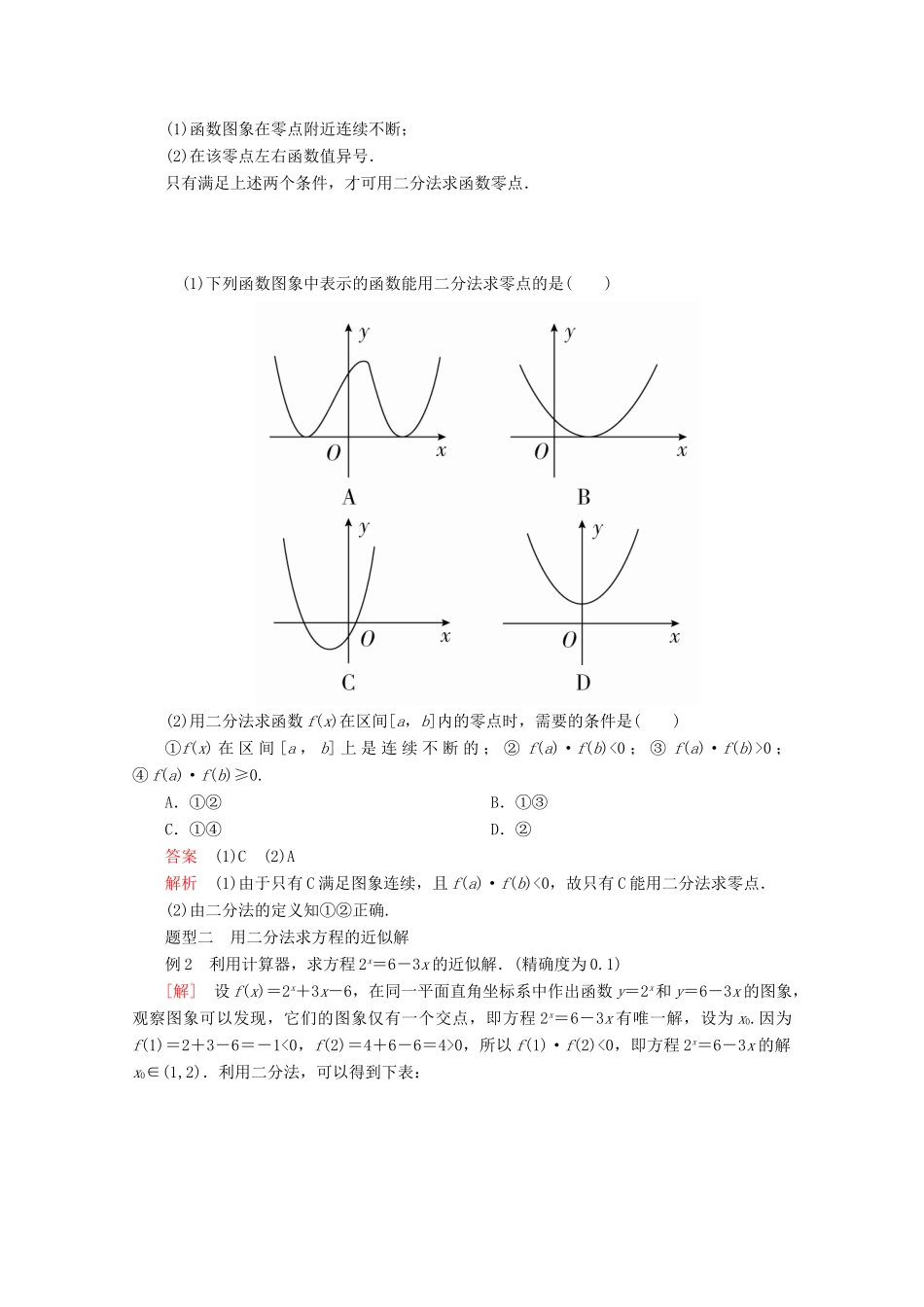
4.5.2 用二分法求方程的近似解(教师独具内容)课程标准:探索用二分法求方程近似解的思路并会画程序框图,能借助计算工具用二分法求方程的近似解,并知道用二分法求方程近似解具有一般性.教学重点:理解二分法的原理及其适用条件,掌握用二分法求方程近似解的一般步骤.教学难点:利用二分法求给定精确度的方程的近似解.【知识导学】知识点一 二分法的概念对于在区间[a,b]上图象□ 连续不断 且□ f ( a ) f ( b ) < 0 的函数 y=f(x),通过不断地把它的零点所在区间□ 一分为二 ,使所得区间的两个端点逐步□ 逼近零点 ,进而得到零点近似值的方法叫做二分法.知识点二 用二分法求方程近似解的步骤给定精确度 ε,用二分法求函数 y=f(x)零点 x0的近似值的一般步骤如下:(1)确定零点 x0的初始区间[a,b],验证□ f ( a ) f ( b ) < 0 .(2)求区间(a,b)的□ 中点 C . (3)计算 f(c),并进一步确定零点所在的区间:① 若 f(c)=0(此时 x0=c),则□ c 就是函数的零点;② 若 f(a)f(c)<0(此时 x0∈□ ( a , c ) ),则令 b=c;③ 若 f(c)f(b)<0(此时 x0∈(c,b)),则令 a=C.(4)判断是否达到精确度 ε:若|a-b|<ε,则得到零点近似值 a(或 b);否则重复步骤(2)~(4).【新知拓展】1.用二分法求函数零点近似值的方法仅适用于函数的变号零点(曲线通过零点时,函数值的符号变号),对函数的不变号零点(曲线通过零点时,函数值的符号不变号)不适用.如求函数 f(x)=(x-1)2的零点近似值就不能用二分法.2.用二分法求函数零点的近似值时,要根据函数的性质尽可能地找到含有零点的更小的区间,这样可以减少用二分法的次数,减少计算量.3.二分法采用逐步逼近的思想,使区间逐步缩小,使函数零点所在的范围逐步缩小,也就是逐渐逼近函数的零点.当区间长度小到一定程度时,就得到近似值.4.由|a-b|<ε,可知区间[a,b]中任意一个值都是零点 x0的满足精确度 ε 的近似值.为了方便,这里统一取区间端点 a(或 b)作为零点的近似值.精确度与精确到是不一样的概念.比如得数是 1.25 或 1.34,精确到 0.1 都是通过四舍五入后保留一位小数得 1.3.而“精确度为 0.1” 指 零 点 近 似 值 所 在 区 间 [a , b] 满 足 |a - b|<0.1 , 比 如 零 点 近 似 值 所 在 区 间[1.25,1.34].若精确度为 0.1,则近似值可以是 1.25,也可以是 1.34...