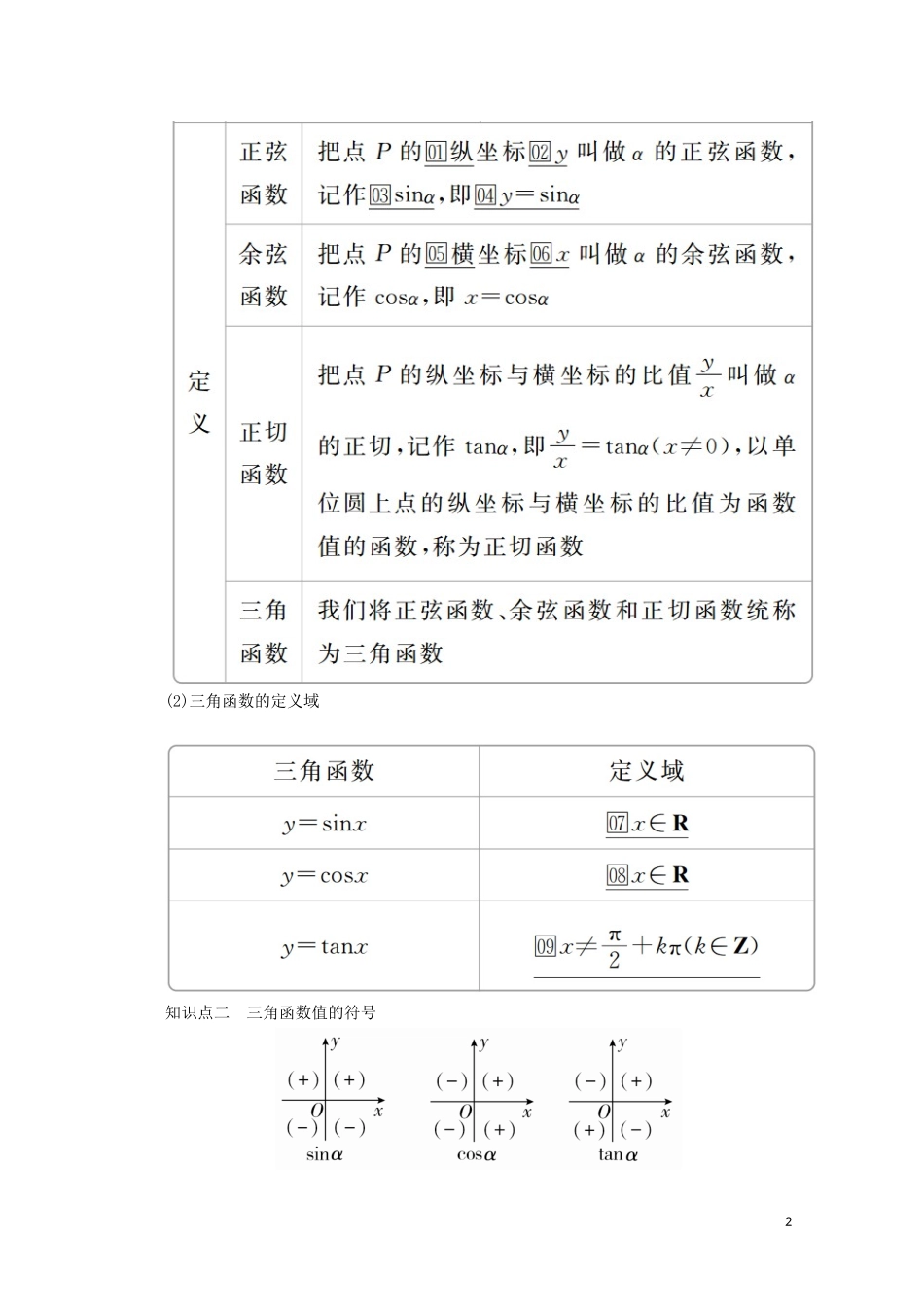
5.2.1 三角函数的概念(教师独具内容)课程标准:1.借助单位圆理解三角函数(正弦、余弦、正切)的定义.2.掌握正弦、余弦、正切函数在各象限内的符号.3.理解终边相同的角的同一三角函数值相等.教学重点:三角函数的定义;三角函数在各象限内的符号.教学难点:任意角的三角函数的定义的建构过程.【知识导学】知识点一 三角函数的概念(1)单位圆中三角函数的定义1(2)三角函数的定义域知识点二 三角函数值的符号2规律:一全正、二正弦、三正切、四余弦.知识点三 诱导公式(一)【新知拓展】(1)三角函数值是比值,是一个实数,这个实数的大小与点 P(x,y)在终边上的位置无关,只与角 α 的终边位置有关,即三角函数值的大小只与角有关.(2)终边相同的角的同名三角函数值相等.1.判一判(正确的打“√”,错误的打“×”)(1)若 α=β+720°,则 cosα=cosβ.( )(2)若 sinα=sinβ,则 α=β.( )(3)已知 α 是三角形的内角,则必有 sinα>0.( )答案 (1)√ (2)× (3)√2.做一做(1)若 sinα<0,且 tanα<0,则 α 在( )A.第一象限 B.第二象限C.第三象限 D.第四象限(2)若角 α 的终边经过点 P(5,-12),则 sinα=________,cosα=________,tanα=________.(3)tan405°-sin450°+cos750°=________.(4)sin2·cos3·tan4 的值的符号为________.答案 (1)D (2)- - (3) (4)负题型一 三角函数的定义例 1 已知角 α 的终边经过点 P(-4a,3a)(a≠0),求 sinα,cosα,tanα 的值.[解] r==5|a|,若 a>0,则 r=5a,角 α 在第二象限,sinα===,cosα===-,tanα===-;若 a<0,则 r=-5a,角 α 在第四象限,sinα=-,cosα=,tanα=-.[条件探究] 在本例中,若将题设条件改为:已知角 α 的终边在直线 y=x 上,问题不变,怎样求解?解 因为角 α 的终边在直线 y=x 上,3所以可设 P(a,a)(a≠0)为角 α 终边上任意一点.则 r= =2|a|(a≠0).若 a>0,则 α 为第一象限角,r=2a,sinα==,cosα==,tanα==.若 a<0,则 α 为第三象限角,r=-2a,sinα==-,cosα==-,tanα==.金版点睛利用三角函数的定义求值的策略(1)已知角 α 的终边在直线上求 α 的三角函数值时,常用的解题方法有以下两种:方法一:先利用直线与单位圆相交,求出交点坐标,然后再利用正、余弦函数的定义求出相应三角函数值.方法二:在 α 的终边上...