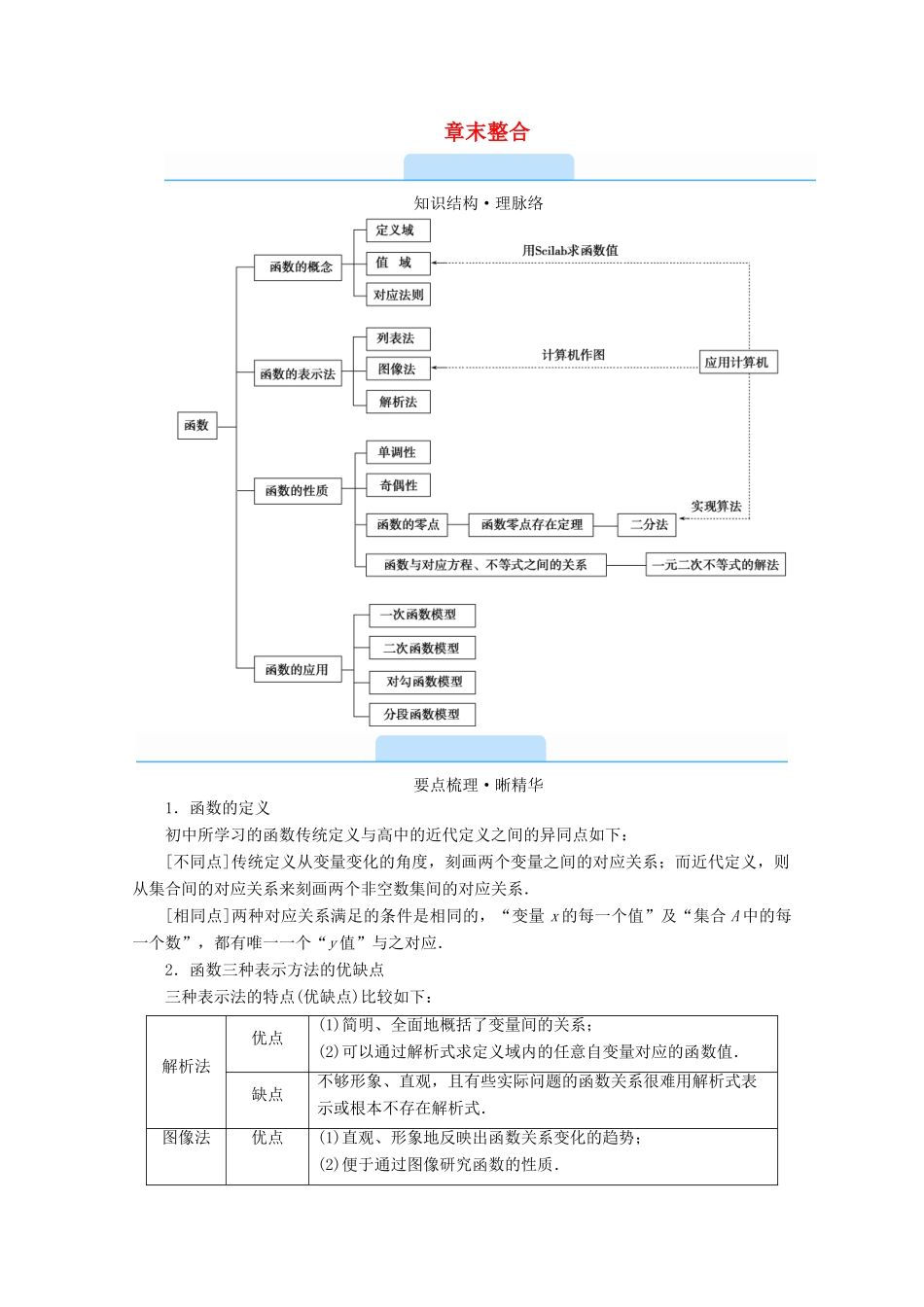
章末整合知识结构·理脉络要点梳理·晰精华1.函数的定义初中所学习的函数传统定义与高中的近代定义之间的异同点如下:[不同点]传统定义从变量变化的角度,刻画两个变量之间的对应关系;而近代定义,则从集合间的对应关系来刻画两个非空数集间的对应关系.[相同点]两种对应关系满足的条件是相同的,“变量 x 的每一个值”及“集合 A 中的每一个数”,都有唯一一个“y 值”与之对应.2.函数三种表示方法的优缺点三种表示法的特点(优缺点)比较如下:解析法优点(1)简明、全面地概括了变量间的关系;(2)可以通过解析式求定义域内的任意自变量对应的函数值.缺点不够形象、直观,且有些实际问题的函数关系很难用解析式表示或根本不存在解析式.图像法优点(1)直观、形象地反映出函数关系变化的趋势;(2)便于通过图像研究函数的性质.缺点只能近似地得到自变量对应的函数值,有时误差较大.列表法优点查询方便,不需计算便可直接得出自变量对应的函数值.缺点(1)只能表示有限个数的函数关系;(2)数较多时使用不方便.并不是所有的函数都能用解析式表示(事实上,图像法也不适用于所有函数,如 D(x)=列表法虽在理论上适用于所有函数,但对于自变量有无数个取值的情况,列表法只能表示函数的一个概况或片段.)3.常见函数的值域(1)一次函数 y=kx+b(k≠0)的值域为 R.(2)二次函数 y=ax2+bx+c(a≠0):当 a>0 时,值域为,当 a<0 时,值域为.(3)反比例函数 y=(k≠0)的值域为{y∈R|y≠0}.4.函数单调性和奇偶性的重要结论(1)当 f(x),g(x)同为增(减)函数时,f(x)+g(x)则为增(减)函数.(2)奇函数在对称的两个区间上有相同的单调性,偶函数在对称的两个区间上有相反的单调性.(3)f(x)为奇函数⇔f(x)的图像关于原点对称;f(x)为偶函数⇔f(x)的图像关于 y 轴对称.(4)偶函数的和、差、积、商是偶函数,奇函数的和、差是奇函数,积、商是偶函数,奇函数与偶函数的积、商是奇函数.(5)定义在(-∞,+∞)上的奇函数的图像必过原点即有 f(0)=0.存在既是奇函数,又是偶函数的函数 f(x)=0.(6)f(x)+f(-x)=0⇔f(x)为奇函数;f(x)-f(-x)=0⇔f(x)为偶函数.5.函数的零点(1)函数零点的定义对于函数 y=f(x)(x∈D),使 f(x)=0 的实数 x 称为函数 y=f(x)(x∈D)的零点.(2)几个等价关系方程 f(x)=0 有实数根⇔函数 y=f(x)的图像与 x 轴有交点⇔函数 y=f(x)有零点.(3)函数零点的判定如果函数 y=f(x)在区间[a,b]上的图像...