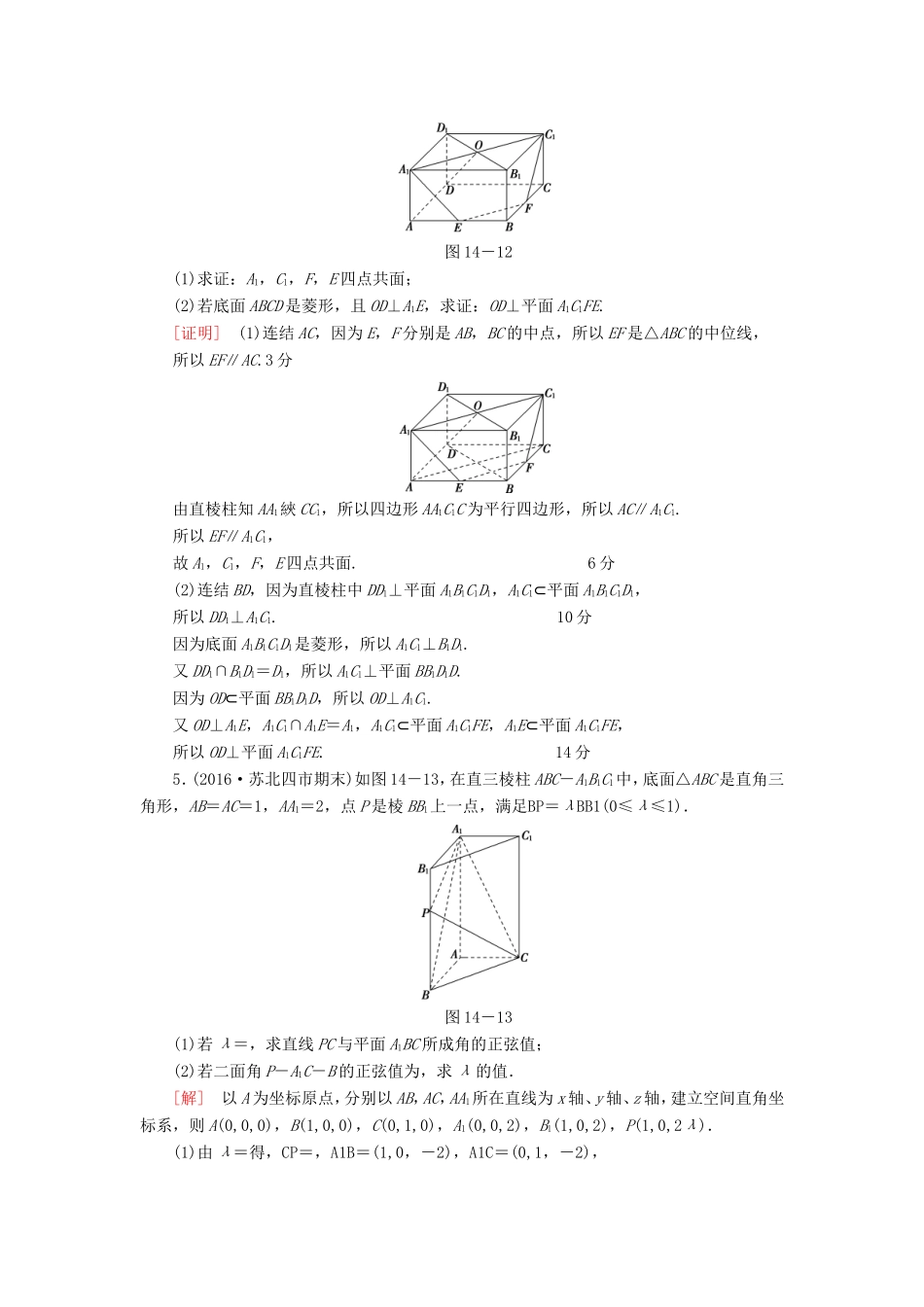
专题限时集训(十五)高考中的立体几何(建议用时:45分钟)1.(2014·江苏高考)如图14-9,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.图14-9求证:(1)直线PA∥平面DEF;(2)平面BDE⊥平面ABC.[证明](1)因为D,E分别为棱PC,AC的中点,所以DE∥PA.3分又因为PA⊄平面DEF,DE⊂平面DEF,所以直线PA∥平面DEF.6分(2)因为D,E,F分别为棱PC,AC,AB的中点,PA=6,BC=8,所以DE∥PA,DE=PA=3,EF=BC=4.又因为DF=5,故DF2=DE2+EF2,所以∠DEF=90°,即DE⊥EF.10分又PA⊥AC,DE∥PA,所以DE⊥AC.因为AC∩EF=E,AC⊂平面ABC,EF⊂平面ABC,所以DE⊥平面ABC.又DE⊂平面BDE,所以平面BDE⊥平面ABC.14分2.如图14-10,在三棱锥P-ABC中,点E,F分别是棱PC,AC的中点.图14-10(1)求证:PA∥平面BEF;(2)若平面PAB⊥平面ABC,PB⊥BC,求证:BC⊥PA.[证明](1)在△PAC中,E,F分别是PC,AC的中点,所以PA∥EF,3分又PA⊄平面BEF,EF⊂平面BEF,所以PA∥平面BEF.6分(2)在平面PAB内过点P作PD⊥AB,垂足为D,因为平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PD⊂平面PAB,所以PD⊥平面ABC,又BC⊂平面ABC,所以PD⊥BC,10分又PB⊥BC,PD∩PB=P,PD⊂平面PAB,PB⊂平面PAB,所以BC⊥平面PAB,又PA⊂平面PAB,所以BC⊥PA.14分3.如图14-11,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA垂直于底面ABCD,PA=AD=AB=2BC=2,M,N分别为PC,PB的中点.图14-11(1)求证:PB⊥DM;(2)求点B到平面PAC的距离.[解](1)证明:因为N是PB的中点,PA=AB,所以AN⊥PB,因为AD⊥平面PAB,所以AD⊥PB,又因为AD∩AN=A,3分从而PB⊥平面ADMN,因为DM⊂平面ADMN,所以PB⊥DM.6分(2)连结AC,过B作BH⊥AC,因为PA⊥底面ABCD,所以平面PAC⊥底面ABCD,所以BH是点B到平面PAC的距离.12分在Rt△ABC中,BH==.14分4.(2016·苏州期末)如图14-12,在直四棱柱ABCD-A1B1C1D1中,E,F分别是AB,BC的中点,A1C1与B1D1交于点O.图14-12(1)求证:A1,C1,F,E四点共面;(2)若底面ABCD是菱形,且OD⊥A1E,求证:OD⊥平面A1C1FE.[证明](1)连结AC,因为E,F分别是AB,BC的中点,所以EF是△ABC的中位线,所以EF∥AC.3分由直棱柱知AA1綊CC1,所以四边形AA1C1C为平行四边形,所以AC∥A1C1.所以EF∥A1C1,故A1,C1,F,E四点共面.6分(2)连结BD,因为直棱柱中DD1⊥平面A1B1C1D1,A1C1⊂平面A1B1C1D1,所以DD1⊥A1C1.10分因为底面A1B1C1D1是菱形,所以A1C1⊥B1D1.又DD1∩B1D1=D1,所以A1C1⊥平面BB1D1D.因为OD⊂平面BB1D1D,所以OD⊥A1C1.又OD⊥A1E,A1C1∩A1E=A1,A1C1⊂平面A1C1FE,A1E⊂平面A1C1FE,所以OD⊥平面A1C1FE.14分5.(2016·苏北四市期末)如图14-13,在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AB=AC=1,AA1=2,点P是棱BB1上一点,满足BP=λBB1(0≤λ≤1).图14-13(1)若λ=,求直线PC与平面A1BC所成角的正弦值;(2)若二面角P-A1C-B的正弦值为,求λ的值.[解]以A为坐标原点,分别以AB,AC,AA1所在直线为x轴、y轴、z轴,建立空间直角坐标系,则A(0,0,0),B(1,0,0),C(0,1,0),A1(0,0,2),B1(1,0,2),P(1,0,2λ).(1)由λ=得,CP=,A1B=(1,0,-2),A1C=(0,1,-2),设平面A1BC的法向量为n1=(x1,y1,z1),由得3分不妨取z1=1,则x1=y1=2,从而平面A1BC的一个法向量为n1=(2,2,1).设直线PC与平面A1BC所成的角为θ,则sinθ=|cos〈CP,n1〉|==,所以直线PC与平面A1BC所成角的正弦值为.6分(2)设平面PA1C的法向量为n2=(x2,y2,z2),A1P=(1,0,2λ-2),由得不妨取z2=1,则x2=2-2λ,y2=2,所以平面PA1C的法向量为n2=(2-2λ,2,1).10分则cos〈n1,n2〉=,又因为二面角P-A1C-B的正弦值为,所以=,化简得λ2+8λ-9=0,解得λ=1或λ=-9(舍去),故λ=1.14分6.(2016·苏锡常镇调研一)如图14-14,在长方体ABCD-A1B1C1D1中,AA1=AB=2AD=2,点E是AB的中点,F是D1E上的一点,D1F=2FE.图14-14(1)证明:平面DFC⊥平面D1EC;(2)求二面角A-DF-C的大小.[解](1)证明:以D为原点,分别以DA,DC,DD1所在直线为x...