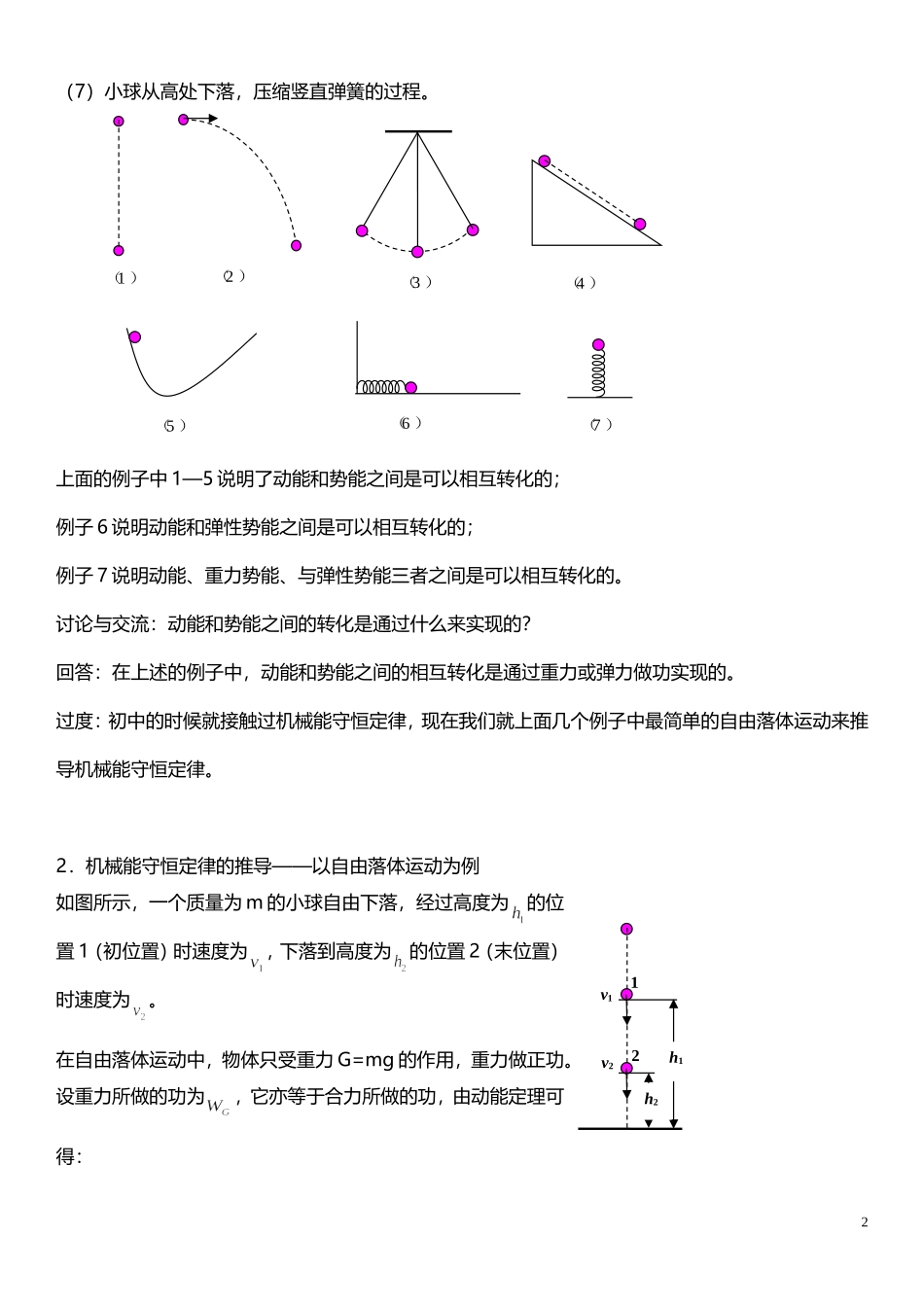
《机械能守恒定律》的教学设计[教学目标]1.掌握机械能守恒定律,知道它的含义和适用条件。2.学会机械能守恒定律解决力学问题,知道应用这个定律的解题步骤,知道用这个定律处理问题的优点。第一课时[教学目标]1.知道动能和势能间可以相互转化。2.能够推导动能与重力势能的转化守恒。3.知道机械能守恒的条件,在具体的环境中能够判断机械能是否守恒。[教学重点]在具体的环境中判断机械能守恒。[教学过程]动能和势能统称为机械能,其中势能包括重力势能和弹性势能。1.动能和势能之间可以相互转化。(以实例的形式引入)列举生活中常见的动能和势能之间相互转化的现象:教材79页。(1)自由落体运动(直线运动)。(2)平抛运动(曲线运动)。(3)单摆的摆动过程。(4)物体在光滑斜面上自由下滑(斜面固定)。(5)物体由一个光滑曲面滚下,然后滚上另一个光滑曲面。(6)光滑水平面放置的压缩弹簧将小球弹出。1(7)小球从高处下落,压缩竖直弹簧的过程。上面的例子中1—5说明了动能和势能之间是可以相互转化的;例子6说明动能和弹性势能之间是可以相互转化的;例子7说明动能、重力势能、与弹性势能三者之间是可以相互转化的。讨论与交流:动能和势能之间的转化是通过什么来实现的?回答:在上述的例子中,动能和势能之间的相互转化是通过重力或弹力做功实现的。过度:初中的时候就接触过机械能守恒定律,现在我们就上面几个例子中最简单的自由落体运动来推导机械能守恒定律。2.机械能守恒定律的推导——以自由落体运动为例如图所示,一个质量为m的小球自由下落,经过高度为的位置1(初位置)时速度为,下落到高度为的位置2(末位置)时速度为。在自由落体运动中,物体只受重力G=mg的作用,重力做正功。设重力所做的功为,它亦等于合力所做的功,由动能定理可得:(1)(2)(3)(4)(5)(6)(7)2h1h2v1v212(1)另一方面,由重力做功与重力势能关系知道,(2)由上面两式可得:可见,在这个运动过程中(从位置1到位置2),重力做了多少功,就有多少功转化为等量的动能。即动能增加了多少,重力势能就减少了多少。表达式二:移项可得:,即(表达式一)上式的左边两项分别表示小球在位置2(末态)的动能和重力势能,相加在一起表示小球在位置2(末态)的机械能;等号右边的两项分别表示小球在位置1(初态)的动能和重力势能,相加在一起表示小球在位置1(初态)的机械能。因此对于上式,我们可以理解为:末态的机械能与初态的机械能是相等的,即机械能在小球的运动过程中保持不变。那么,我们还可以推广到任意时刻或任意位置小球的动能和重力势能之和保持不变。至此,我们推导出了机械能守恒定律的两个表达式。实际上,我们还可以由其他的模型来证明。<学生活动>试用上面提到的实例3推导机械能守恒定律。解答:与上面用自由落体运动的推导过程完全相同。讨论与交流:教材80页,机械能守恒定律成立的条件是什么?3.探讨机械能守恒的条件在上面的推导过程中,我们用到了两个规律:一个是动能定理,一个是重力做功与重力势能之间的关3系。两个规律结合在一起之所以能推导出机械能守恒定律,是因为在应用动能定理的时候有因此机械能守恒的条件是:即:如果重力的功等于合力的功,也可以理解为只有重力做功,机械能就是守恒的。我们用这个条件去考察上面的实例1—5:(1)只受重力,重力的功等于合力的功,机械能守恒;(2)只受重力,重力的功等于合力的功,机械能守恒;(3)受重力和绳拉力,但绳拉力不做功,只有重力做功,因此有重力功等于合力功,机械能守恒;(4)受重力和支持力,但支持力不做功,只有重力做功,因此有重力功等于合力功,机械能守恒;(5)受重力和支持力,但支持力不做功,只有重力做功,因此有重力功等于合力功,机械能守恒;小结:只有重力做功,机械能守恒。我们还可以这样来理解重力的功:它只是使物体的动能与重力势能之间发生了转化,即只是使能量在机械能内部之间转化,重力做功不改变机械能总量,因而机械能是守恒的。(6)受重力、支持力和弹簧弹力,但只有弹力做功,因此有弹力功等于合力功,机械能守恒;(7)受重力和弹簧弹力,弹簧弹...