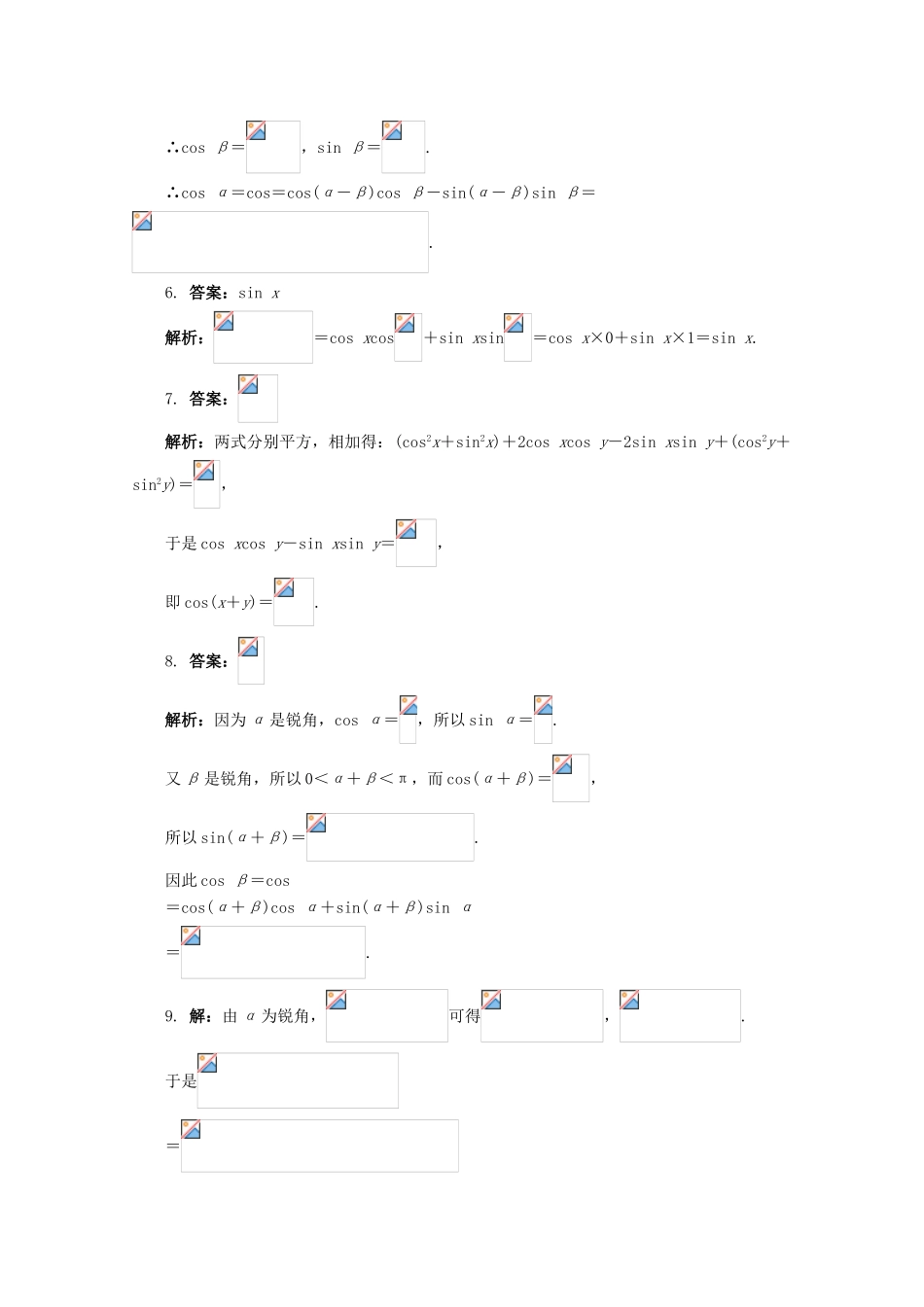
高中数学5.1.1两角和与差的正弦和余弦第一课时同步练习湘教版必修21.下列四个命题中是假命题的是()A.存在这样的α和β的值使得cos(α+β)=cosαcosβ+sinαsinβB.不存在无穷多个α和β的值使得cos(α+β)=cosαcosβ+sinαsinβC.对于任意的α和β有cos(α+β)=cosαcosβ-sinαsinβD.不存在这样的α和β的值使得cos(α+β)≠cosαcosβ-sinαsinβ2.已知θ∈,cosθ=,则等于()A.B.C.D.3.化简sin(x+y)sin(x-y)+cos(x+y)cos(x-y)的结果是()A.sin2xB.cos2yC.-cos2xD.-cos2y4.已知在△ABC中,满足tanAtanB>1,则这个三角形一定是()A.正三角形B.等腰直角三角形C.锐角三角形D.钝角三角形5.已知sin(α-β)=,α-β是第一象限角,tanβ=,β是第三象限角,则cosα等于()A.B.C.D.6.化简__________.7.已知cosx+cosy=,sinx-siny=,则cos(x+y)=__________.8.已知锐角α,β满足cosα=,cos(α+β)=,则cosβ=__________.9.已知,α为锐角,求cosα的值.10.已知,,且<α<π,0<β<,求的值.参考答案1.答案:B解析:当α=2kπ,β=2kπ(k∈Z)时,cos(α+β)=cosαcosβ+sinαsinβ,故A对,B错;由和角余弦公式易知C,D均对.2.答案:B解析:∵θ∈,cosθ=,∴.∴=cosθcos+sinθsin=.3.答案:B解析:原式=cos(x+y)cos(x-y)+sin(x+y)sin(x-y)=cos=cos2y.4.答案:C解析:由tanAtanB>1>0知tanA>0,tanB>0,即A,B都是锐角.又∵,∴sinAsinB>cosAcosB.得到cos(A+B)<0.∴cos(π-C)<0,即cosC>0,则C也是锐角.因此△ABC是锐角三角形.5.答案:D解析:∵α=(α-β)+β,∴cosα=cos.∵α-β是第一象限角,sin(α-β)=,∴cos(α-β)=.又∵B是第三象限角,tanβ=,∴sinβ=cosβ.又∵sin2β+cos2β=1,∴cos2β=,sin2β=.∴cosβ=,sinβ=.∴cosα=cos=cos(α-β)cosβ-sin(α-β)sinβ=.6.答案:sinx解析:=cosxcos+sinxsin=cosx×0+sinx×1=sinx.7.答案:解析:两式分别平方,相加得:(cos2x+sin2x)+2cosxcosy-2sinxsiny+(cos2y+sin2y)=,于是cosxcosy-sinxsiny=,即cos(x+y)=.8.答案:解析:因为α是锐角,cosα=,所以sinα=.又β是锐角,所以0<α+β<π,而cos(α+β)=,所以sin(α+β)=.因此cosβ=cos=cos(α+β)cosα+sin(α+β)sinα=.9.解:由α为锐角,可得,.于是==.10.解:∵<α<π,0<β<,∴,.又∵,,∴,.∴==.