高中数学 第三章 指数函数和对数函数 3.2 指数扩充及其运算性质 3.3 指数函数教案 北师大版必修1-北师大版高一必修1数学教案VIP免费

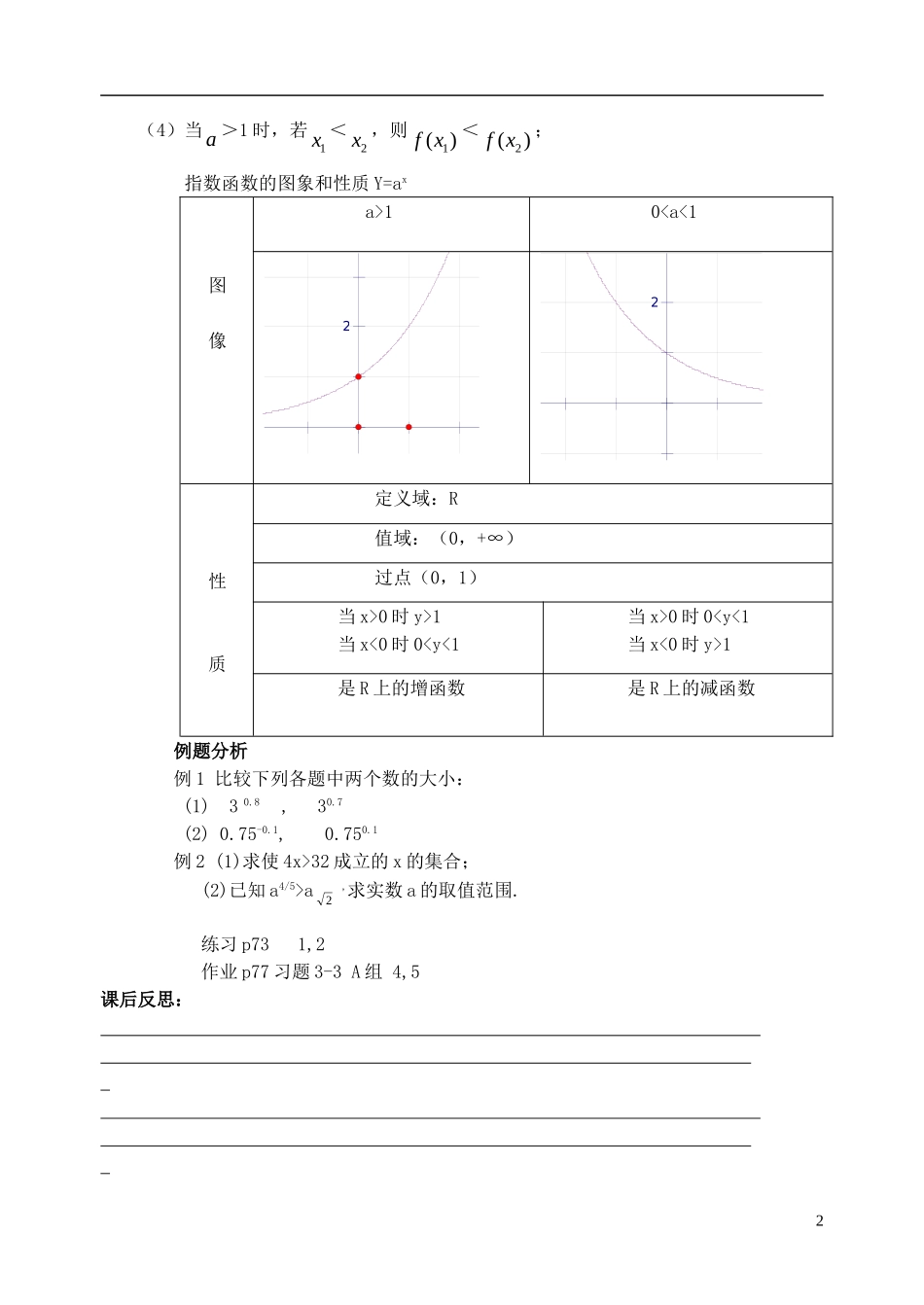
3.3指数函数第一课时问题：1：从画出的图象中，你能发现函数的图象与底数间有什么样的规律.从图上看xya（a＞1）与xya（0＜a＜1）两函数图象的特征.问题2：根据函数的图象研究函数的定义域、值域、特殊点、单调性、最大（小）值、奇偶性.问题3：指数函数xya（a＞0且a≠1），当底数越大时，函数图象间有什么样的关系.图象特征函数性质a＞10＜a＜1a＞10＜a＜1向x轴正负方向无限延伸函数的定义域为R图象关于原点和y轴不对称非奇非偶函数函数图象都在x轴上方函数的值域为R+函数图象都过定点（0，1）0a=1自左向右，图象逐渐上升自左向右，图象逐渐下降增函数减函数在第一象限内的图象纵坐标都大于1在第一象限内的图象纵坐标都小于1x＞0，xa＞1x＞0，xa＜1在第二象限内的图象纵坐标都小于1在第二象限内的图象纵坐标都大于1x＜0，xa＜1x＜0，xa＞15．利用函数的单调性，结合图象还可以看出：（1）在[,]xabfxa上,()=（a＞0且a≠1）值域是[(),()][(),()];fafbfbfa或（2）若0,xfxfxx则()1;()取遍所有正数当且仅当R;（3）对于指数函数()xfxa（a＞0且a≠1），总有(1);fa1(1)xyaa(01)xyaa0（4）当a＞1时，若1x＜2x，则1()fx＜2()fx；指数函数的图象和性质Y=ax图像a>100时y>1当x<0时00时01是R上的增函数是R上的减函数例题分析例1比较下列各题中两个数的大小：(1)30.8,30.7(2)0.75-0.1,0.750.1例2(1)求使4x>32成立的x的集合；(2)已知a4/5>a2,求实数a的取值范围.练习p731,2作业p77习题3-3A组4,5课后反思：2第二课时（1）提出问题指数函数y=ax(a>0,a≠1)底数a对函数图象的影响，我们通过两个实例来讨论a>1和0b>1时，（1）当x<0时，总有ax0时，总ax>bx>1有；（4）指数函数的底数a越大，当x>0时，其函数值增长越快。动手实践二：分别画出底数为0.2,0.3,0.5,2,3,5的指数函数图象.总结y=ax(a>0,a≠1)，a对函数图象变化的影响。结论：（1）当X>0时,a越大函数值越大；当x<0时,a越大函数值越小。（2）当a>1时指数函数是增函数，当x逐渐增大时，函数值增大得越来越快；当01.80=1,0.81.6<0.80=1,所以1.80.6>0.81.6(2)解由指数函数性质知(1/3)-2/3>1,2-3/5<1,所以(1/3)-2/3>2-3/53例5已知-11，因此有3-x>1又0<0.5<1，因而有0<0.5-x<1故3-x>0.5-x（法2）设a=-x>0,函数f(x)=xa当x>0时为增函数，而3>0.5>0,故f(3)>f(0.5)即3-x>0.5-x小结：在比较两个指数幂大小时，常利用指数函数和幂函数的单调性。相同底数比较指数，相同指数比较底数。故常用到中间量“1”。练习1，2作业习题3-3B组1,2课后反思：4