高中数学 142正弦函数、余弦函数的性质(3)课件 新人教A版必修4 课件VIP免费

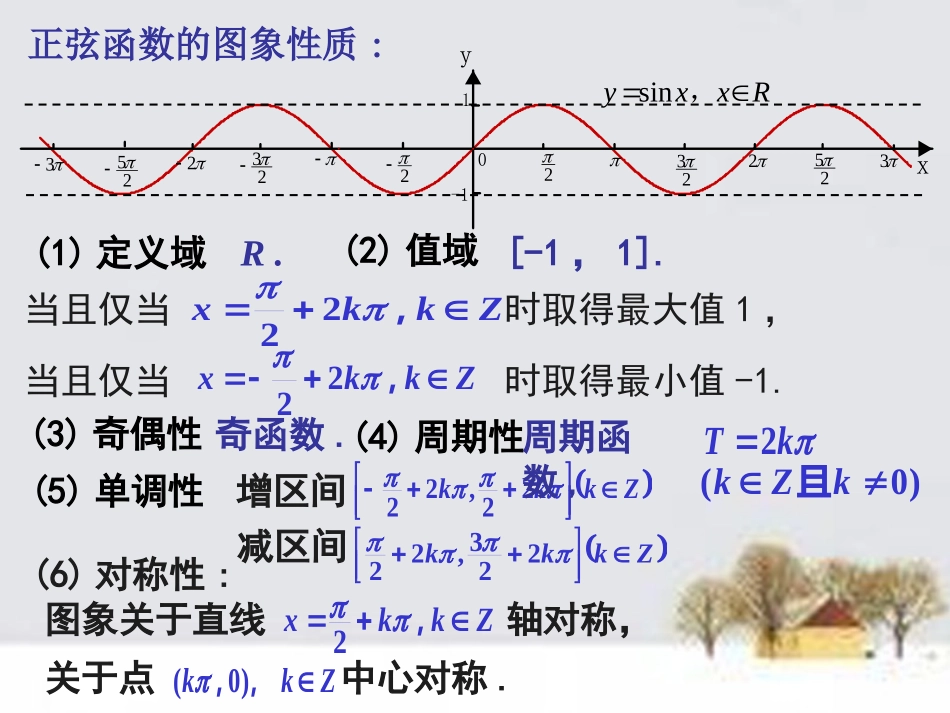
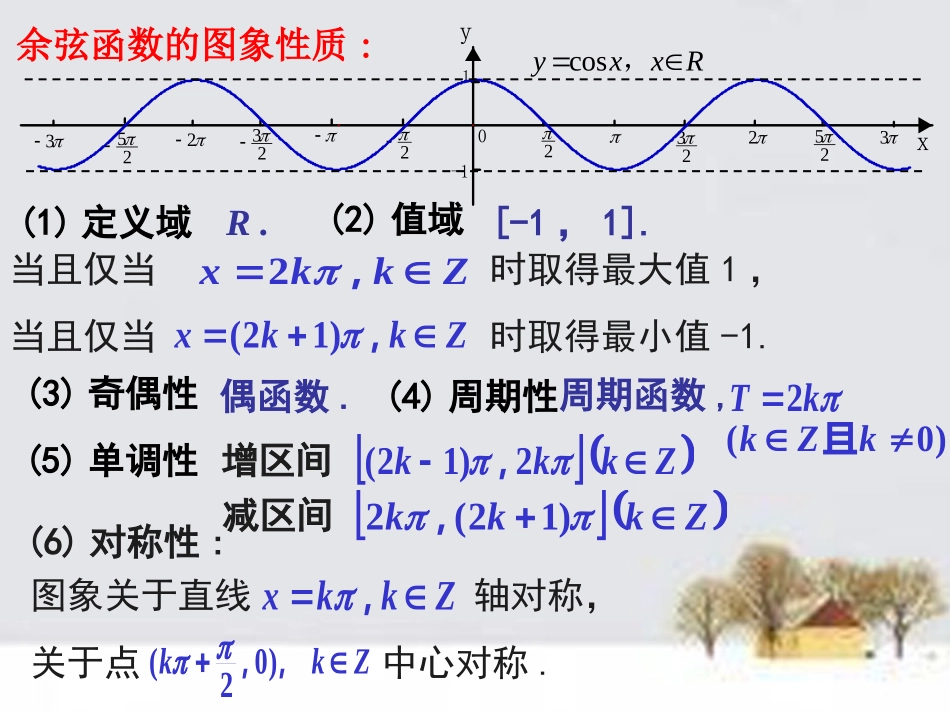
1.4.2正弦函数、余弦函数的性质（3）正弦函数的图象性质:(1)定义域(2)值域R.[-1，1].当且仅当时取得最大值1，当且仅当时取得最小值-1.Zkkx，22Zkkx，22(3)奇偶性奇函数.(5)单调性增区间减区间Zkkk22,22Zkkk223,22(6)对称性:图象关于直线轴对称，关于点中心对称.Zkkx，2Zkk，，)0((4)周期性周期函数,Rxxy，sin32532522322322-11yx02Tk(0)kZk且余弦函数的图象性质:(1)定义域(2)值域R.[-1，1].当且仅当时取得最大值1，当且仅当时取得最小值-1.Zkkx，2Zkkx，)12((3)奇偶性偶函数.(5)单调性增区间减区间(6)对称性:图象关于直线轴对称，关于点中心对称.Zkkx，Zkk，，)02(Zkkk2)12(，Zkkk)12(2，(4)周期性周期函数,32532522322322-11yx0Rxxy，cos2Tk(0)kZk且单调递增区间.sin(2)3yx(1)求函数解：2,3ux令sinyu则23uxR在上是增函数，由复合函数“同增异减”原则知，sinyu是增函数.22,()22kukkZ，222,()232kxkkZ即，5[,],().1212kkkZsin(2)3yx故的增区间为例1.cos(2)3yx(2)求函数单调递增区间.课堂练习：《乐学》P18例1例2求函数y＝cos2x＋4sinx的最值及取到最大值和最小值时的x的集合．解y＝cos2x＋4sinx＝1－sin2x＋4sinx＝－sin2x＋4sinx＋1＝－(sinx－2)2＋5.∴当sinx＝1，即x＝2kπ＋π2，k∈Z时，ymax＝4；当sinx＝－1时，即x＝2kπ－π2，k∈Z时，ymin＝－4.所以ymax＝4，此时x的取值集合是{x|x＝2kπ＋π2，k∈Z}；ymin＝－4，此时x的取值集合是{x|x＝2kπ－π2，k∈Z}．课堂练习：《乐学》P19例3小结形如f(x)＝asin2x＋bsinx＋c(a≠0)的函数值域问题，可以通过换元转化为二次函数g(t)＝at2＋bt＋c在闭区间[－1,1]上的最值问题．要注意，正、余弦函数值域的有界性，即当x∈R时，－1≤sinx≤1，－1≤cosx≤1对值域的影响．图象设函数)(),0)(2sin()(xfyxxf.8x的一条对称轴为直线；求)1(；的单调区间求函数)()2(xfy解：，图象的对称轴是函数)(8)1(xfyx，1)82sin(.)(24Zkk0.43例3.得，由43)2(.)432sin()(xxf，，Zkkxk2243222，，Zkkxk858.]858[Zkkk，，函数增区间为解：，，Zkkxk23243222.8985Zkkxk，增区间减区间Zkkk22,22Zkkk223,22∵y=sinx的单调区间为:单调增、减区间由下面不等式确定:)432sin()(xxf解得：.]8985[Zkkk，，函数减区间为课堂练习：《乐学》P33变式4课后作业1.《乐学》1.4.2